题目内容
15.计算:(1)-21$\frac{2}{3}$+3$\frac{3}{4}$-$\frac{1}{3}$+0.25;
(2)(-2)2+2×[(-3)2-3÷$\frac{1}{2}$];
(3)77°53′26″+33°18′44″;
(4)27°17′32″×5.
分析 (1)直接分类计算,再进一步合并即可;
(2)先算乘方和除法,再算括号里面的减法,再算乘法,最后算加法;
(3)(4)利用度分秒的四则计算方法计算,注意满60进一即可.
解答 解:(1)原式=-22+4
=-18;
(2)原式=4+2×(9-6)
=4+2×3
=4+6
=10;
(3)原式=111°12′10″;
(4)原式=136°27′40″.
点评 此题考查有理数的混合运算与度分秒的计算,掌握运算顺序,正确判定运算符号计算即可.

练习册系列答案
相关题目
5.已知$\frac{b}{a}$=$\frac{2}{3}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
7.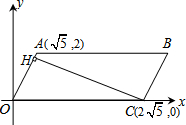 如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
 如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )| A. | B点坐标为(2$\sqrt{5}$,2) | B. | B点坐标为(3$\sqrt{5}$,2) | C. | S?OABC=2$\sqrt{5}$ | D. | CH=$\frac{4}{3}$$\sqrt{5}$ |
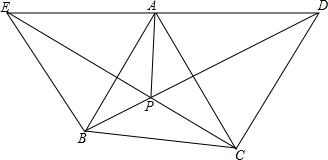 锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.
锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.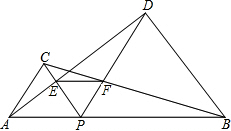 如图所示,P是线段AB上一点,△APC和△BPD都是正三角形,AD与PC交于点E,BC与PD交于点F,连接EF,试探究△PEF的形状.
如图所示,P是线段AB上一点,△APC和△BPD都是正三角形,AD与PC交于点E,BC与PD交于点F,连接EF,试探究△PEF的形状.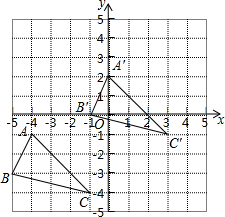 如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).
如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2). 一张长为 a cm,宽为 b cm,周长为32cm的长方形硬纸片,四个角上各剪去一个边长为1cm的小正方形(如图),然后折成一个无盖纸盒(纸板的厚度忽略不计).
一张长为 a cm,宽为 b cm,周长为32cm的长方形硬纸片,四个角上各剪去一个边长为1cm的小正方形(如图),然后折成一个无盖纸盒(纸板的厚度忽略不计).