题目内容
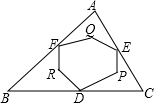 如图,在锐角三角形ABC中,点D、E、F分别是边BC、CA、AB的中点,从每边中点分别作其余两边的垂线,这六条垂线围成六边形DPEQFR,设六边形DPEQFR的面积为S1,△ABC的面积为S,则S1:S=( )
如图,在锐角三角形ABC中,点D、E、F分别是边BC、CA、AB的中点,从每边中点分别作其余两边的垂线,这六条垂线围成六边形DPEQFR,设六边形DPEQFR的面积为S1,△ABC的面积为S,则S1:S=( )| A、3:5 | B、2:3 | C、1:2 | D、1:3 |
分析:过三个中点分别作六边形边的平行线,则此六边形被分割为3个平行四边形,从而得到六边形的面积等于三角形DEF面积的2倍,从而问题可解.
解答: 解:过三个中点分别作六边形边的平行线,交于点M,
解:过三个中点分别作六边形边的平行线,交于点M,
∴六边形DPEQFR被分成平行四边形DPEM,平行四边形DMFR,平行四边形EQFM,
∵DE、EF、DF分别是平行四边形的对角线,
∴S平行四边形DPEM=2S△DEM,S平行四边形DMFR=2S△DFM,S平行四边形EQFM=2S△EFM,
∴S六边形DPEQFR=2S△DEF,
∵△DEF∽△ABC,
∴
=
,
∴S六边形DPEQFR=
S△ABC
∴S1:S=1:2.
故选C.
 解:过三个中点分别作六边形边的平行线,交于点M,
解:过三个中点分别作六边形边的平行线,交于点M,∴六边形DPEQFR被分成平行四边形DPEM,平行四边形DMFR,平行四边形EQFM,
∵DE、EF、DF分别是平行四边形的对角线,
∴S平行四边形DPEM=2S△DEM,S平行四边形DMFR=2S△DFM,S平行四边形EQFM=2S△EFM,
∴S六边形DPEQFR=2S△DEF,
∵△DEF∽△ABC,
∴
| S△DEF |
| S△ABC |
| 1 |
| 4 |
∴S六边形DPEQFR=
| 1 |
| 2 |
∴S1:S=1:2.
故选C.
点评:本题考查了三角形的中位线定理以及平行四边形的判定和性质,是中档题,有一定的难度.

练习册系列答案
相关题目
 如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )
如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )| A、12cm | B、13cm | C、14cm | D、15cm |
 (1)如图,在锐角三角形ABC中,BC=12,
(1)如图,在锐角三角形ABC中,BC=12, 如图,在锐角三角形ABC中,AD⊥BC,AD=12,AC=13,BC=14.则AB=
如图,在锐角三角形ABC中,AD⊥BC,AD=12,AC=13,BC=14.则AB= 如图,在锐角三角形ABC中,AD、CE分别是边BC、AB上的高,垂足分别是D、E,AD、CE相交于点O,若∠B=60°,则∠AOE的度数是( )
如图,在锐角三角形ABC中,AD、CE分别是边BC、AB上的高,垂足分别是D、E,AD、CE相交于点O,若∠B=60°,则∠AOE的度数是( ) 如图,在锐角三角形ABC中,BC=
如图,在锐角三角形ABC中,BC=