题目内容
17.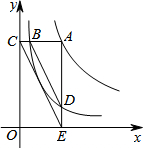 如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$.
如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$.
分析 设点A的坐标为(m,n),则B($\frac{m}{4}$,n),C(0,n),D(m,$\frac{n}{4}$),E(m,0),由此即可得出$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{3}{4}$,结合∠A=∠A即可证出△ABD∽△ACE,再根据相似三角形的性质即可得出$\frac{BD}{CE}$的值.
解答 解:设点A的坐标为(m,n),
∵作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,
∴B($\frac{m}{4}$,n),C(0,n),D(m,$\frac{n}{4}$),E(m,0),
∴AB=$\frac{3}{4}$m,AC=m,AD=$\frac{3}{4}$n,AE=n,
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{3}{4}$.
又∵∠A=∠A,
∴△ABD∽△ACE,
∴$\frac{BD}{CE}$=$\frac{AB}{AC}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了反比例函数图象上点的坐标特征以及相似三角形的判定与性质,根据$\frac{AB}{AC}$=$\frac{AD}{AE}$和∠A=∠A证出△ABD∽△ACE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.△ABC的外心在三角形的内部,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判断 |
9.下列命题中,属于假命题的是( )
| A. | 对顶角相等 | |
| B. | 三角形内角和等于180° | |
| C. | 全等三角形对应角相等 | |
| D. | 有三个角分别对应相等的两个三角形全等 |
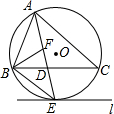 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.