题目内容
10.在 Rt△ABC中.∠C=90°,tanA=$\frac{3}{4}$,AB=10,则BC的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由tanA=$\frac{BC}{AC}$=$\frac{3}{4}$可设BC=3x,则AC=4x,根据AC2+BC2=AB2,即(3x)2+(4x)2=102,求得x的值即可得.
解答 解:如图,
∵Rt△ABC中,tanA=$\frac{BC}{AC}$=$\frac{3}{4}$,
∴设BC=3x,则AC=4x,
∵AC2+BC2=AB2,即(3x)2+(4x)2=102,
解得:x=2或x=-2(舍)
∴BC=3x=6,
故选:B.
点评 本题主要考查解直角三角形,熟练掌握三角函数的定义及勾股定理是解题的关键.

练习册系列答案
相关题目
20.下列运用完全平方公式计算正确的是( )
| A. | (m-1)2=m2-1 | B. | (2a+b)2=2a2+2ab+b2 | ||
| C. | (x2-$\frac{1}{2}$)2=x4-x2+$\frac{1}{4}$ | D. | 3(m+1)2=3m2+2m+1 |
1.|-$\frac{3}{4}$|的相反数是( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
15.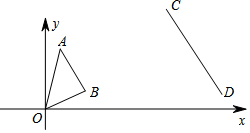 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )| A. | (0,0) | B. | (3,4)或(-6,2) | C. | (5,3)或(-7,1) | D. | 不能确定 |
20.高度每增加1千米,气温就下降2℃,现在地面气温是-10℃,那么离地面高度为7千米的高空的气温是( )
| A. | -4℃ | B. | -14℃ | C. | -24℃ | D. | 14℃ |
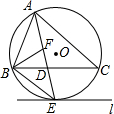 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC. 蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m.
蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m.