题目内容
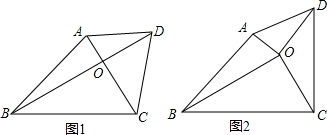
如图1,已知梯形ABCD,AD∥BC,对角线AC、BD互相垂直,则:
(1)证明:AD2+BC2=AB2+CD2.
(2)如图2,当△AOD以点O为旋转中心,逆时针旋转θ度(0<θ<90),问上面的结论是否成立,请说明理由.
(1)证明:AD2+BC2=AB2+CD2.
(2)如图2,当△AOD以点O为旋转中心,逆时针旋转θ度(0<θ<90),问上面的结论是否成立,请说明理由.

考点:旋转的性质,勾股定理
专题:
分析:(1)如图1,证明AD2+BC2=OA2+OB2+OC2+OD2;证明AB2+CD2=OA2+OB2+OC2+OD2,得到AD2+BC2=AB2+CD2.
(2)如图2,作辅助线;证明△AOM∽△DON,得到
=
①;证明△AOD∽△COB,
=
,
=
②,进而得到
=
,故OB•OM=OC•ON.证明AB2=BM2+AM2=OA2+OB2-2OB•OM③,同理可求:CD2=OC2+OD2+2OC•ON④,由③+④得:AB2+CD2=OA2+OB2+OC2+OD2;而AD2+BC2=OA2+OB2+OC2+OD2,得到AD2+BC2=AB2+CD2.
(2)如图2,作辅助线;证明△AOM∽△DON,得到
| AO |
| DO |
| OM |
| ON |
| AO |
| CO |
| DO |
| BO |
| AO |
| DO |
| CO |
| BO |
| OM |
| ON |
| CO |
| BO |
解答: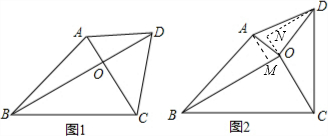 解:(1)如图1,∵AC⊥BD,
解:(1)如图1,∵AC⊥BD,
∴AD2=OA2+OD2,BC2=OB2+OC2,
∴AD2+BC2=OA2+OB2+OC2+OD2;
同理可证:
AB2+CD2=OA2+OB2+OC2+OD2,
∴AD2+BC2=AB2+CD2.
(2)结论AD2+BC2=AB2+CD2,仍然成立;
理由如下:
如图2,过点A作AM⊥BO,过点D作DN⊥CO,
交CO的延长线于点N;
∵∠AOD+∠BOC=180°,
∴∠AOB+∠DOC=180°;而∠DON+∠DOC=180°,
∴∠AOB=∠DON,即∠AOM=∠DON,
∴△AOM∽△DON,
∴
=
①;在图1中,
∵AD∥BC,
∴∠ADO=∠CBO;在图2中,由题意得:
∠ADO=∠CBO,∠AOD=∠COB,
∴△AOD∽△COB,
∴
=
,
=
②,
由①②知:
=
,
∴OB•OM=OC•ON.
由题意得:AB2=BM2+AM2
=(BO-OM)2+AO2-MO2
=OB2-2OB•OM+OM2+OA2-OM2
=OA2+OB2-2OB•OM③,
同理可求:CD2=OC2+OD2+2OC•ON④,
∴由③+④得:
AB2+CD2=OA2+OB2+OC2+OD2;
而AD2+BC2=OA2+OB2+OC2+OD2,
∴AD2+BC2=AB2+CD2.
 解:(1)如图1,∵AC⊥BD,
解:(1)如图1,∵AC⊥BD,∴AD2=OA2+OD2,BC2=OB2+OC2,
∴AD2+BC2=OA2+OB2+OC2+OD2;
同理可证:
AB2+CD2=OA2+OB2+OC2+OD2,
∴AD2+BC2=AB2+CD2.
(2)结论AD2+BC2=AB2+CD2,仍然成立;
理由如下:
如图2,过点A作AM⊥BO,过点D作DN⊥CO,
交CO的延长线于点N;
∵∠AOD+∠BOC=180°,
∴∠AOB+∠DOC=180°;而∠DON+∠DOC=180°,
∴∠AOB=∠DON,即∠AOM=∠DON,
∴△AOM∽△DON,
∴
| AO |
| DO |
| OM |
| ON |
∵AD∥BC,
∴∠ADO=∠CBO;在图2中,由题意得:
∠ADO=∠CBO,∠AOD=∠COB,
∴△AOD∽△COB,
∴
| AO |
| CO |
| DO |
| BO |
| AO |
| DO |
| CO |
| BO |
由①②知:
| OM |
| ON |
| CO |
| BO |
∴OB•OM=OC•ON.
由题意得:AB2=BM2+AM2
=(BO-OM)2+AO2-MO2
=OB2-2OB•OM+OM2+OA2-OM2
=OA2+OB2-2OB•OM③,
同理可求:CD2=OC2+OD2+2OC•ON④,
∴由③+④得:
AB2+CD2=OA2+OB2+OC2+OD2;
而AD2+BC2=OA2+OB2+OC2+OD2,
∴AD2+BC2=AB2+CD2.
点评:该题主要考查了旋转变换、勾股定理等几何知识点及其应用问题;解题的关键是深入观察图形结构特点,数形结合,准确找出图形中隐含的数量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=x2+3x+m(m为常数)的图象与x轴有两个交点,其中一个交点为(-1,0),则另一个交点是( )
| A、(1,0) |
| B、(2,0) |
| C、(-2,0) |
| D、(-3,0) |
如图所示,各正方体的四个数之间有相同的规律,根据此规律,“ ”位置的数是( )
”位置的数是( )

 ”位置的数是( )
”位置的数是( )
| A、144 | B、132 |
| C、168 | D、158 |
30°角的余角的补角是( )
| A、60° | B、150° |
| C、120° | D、不能确定 |
 如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为
如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 如图,点C线段AB的中点,线段AC=10cm,则AB=
如图,点C线段AB的中点,线段AC=10cm,则AB= 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,DF∥AC,AF与DE交于点G,BE与DF交于点H,求证:GH∥AB.
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,DF∥AC,AF与DE交于点G,BE与DF交于点H,求证:GH∥AB.