题目内容
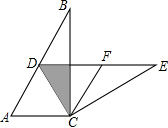 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.(1)求m的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
考点:旋转的性质
专题:
分析:(1)首先证明∠A=60°,AC=DC,判断△DAC为等边三角形,得到∠ACD=60°,即可解决问题.
(2)根据题意,证明AD=AC=λ;再证明DF=CF=λ,得到AD=DF=CF=AC,即可解决问题.
(2)根据题意,证明AD=AC=λ;再证明DF=CF=λ,得到AD=DF=CF=AC,即可解决问题.
解答: 解:(1)如图,∵∠ACB=90°,∠B=30°,
解:(1)如图,∵∠ACB=90°,∠B=30°,
∴AB=2AC(设AC为λ);∠A=60°;
由题意得:AC=DC,
∴△DAC为等边三角形,
∴∠ACD=60°,
∴m=60°.
(2)∵△DAC为等边三角形,
∴AD=AC=λ;
由题意得:DE=AB=2λ;∠DCE=∠ACB=90°;
∵F是DE的中点,
∴DF=CF=λ,
∴AD=DF=CF=AC,
∴四边形ACFD为菱形.
 解:(1)如图,∵∠ACB=90°,∠B=30°,
解:(1)如图,∵∠ACB=90°,∠B=30°,∴AB=2AC(设AC为λ);∠A=60°;
由题意得:AC=DC,
∴△DAC为等边三角形,
∴∠ACD=60°,
∴m=60°.
(2)∵△DAC为等边三角形,
∴AD=AC=λ;
由题意得:DE=AB=2λ;∠DCE=∠ACB=90°;
∵F是DE的中点,
∴DF=CF=λ,
∴AD=DF=CF=AC,
∴四边形ACFD为菱形.
点评:该题主要考查了旋转变换的性质、等边三角形的判定、直角三角形的性质等几何知识点及其应用问题;解题的关键是牢固掌握旋转变换的性质、等边三角形的判定、直角三角形的性质等几何知识点.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
在直线l上顺次取A,B,C,D四点,并且使AB:BC:CD=2:3:4,如果AB中点M与CD中点N的距离是12cm,那么CD的长是( )
| A、4cm | B、6cm |
| C、8cm | D、24cm |
已知二次函数y=x2+3x+m(m为常数)的图象与x轴有两个交点,其中一个交点为(-1,0),则另一个交点是( )
| A、(1,0) |
| B、(2,0) |
| C、(-2,0) |
| D、(-3,0) |
 图中共有线段( )
图中共有线段( )| A、8条 | B、9条 |
| C、10条 | D、11条 |
 如图,AD为△ABC的角平分线,BF⊥AD的延长线于点F,AM⊥AD于A交BC的延长线于M,FC的延长线交AM于E.求证:AE=EM.
如图,AD为△ABC的角平分线,BF⊥AD的延长线于点F,AM⊥AD于A交BC的延长线于M,FC的延长线交AM于E.求证:AE=EM. 如图,点C线段AB的中点,线段AC=10cm,则AB=
如图,点C线段AB的中点,线段AC=10cm,则AB=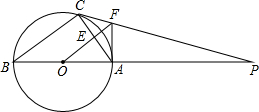 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.