��Ŀ����
15��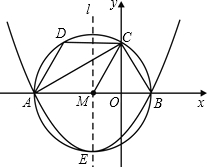 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD����ABΪֱ���ġ�M���ڽ��ı��Σ���A��B��x���ϣ���MBC�DZ߳�Ϊ2�ĵȱ������Σ�����M��ֱ��l��x�ᴹֱ������M�ڵ�E������Ϊ��M���ҵ�Dƽ��$\widehat{AC}$��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD����ABΪֱ���ġ�M���ڽ��ı��Σ���A��B��x���ϣ���MBC�DZ߳�Ϊ2�ĵȱ������Σ�����M��ֱ��l��x�ᴹֱ������M�ڵ�E������Ϊ��M���ҵ�Dƽ��$\widehat{AC}$����1�����A��B��E����������ߵĽ���ʽ��
��2����֤���ı���AMCD�����Σ�
��3�����������������Ƿ����һ��P��ʹ�á�ABP��������ڶ�ֵ5�������ڣ���������еĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1����������������������߶���E�����꣬�����ö���ʽ�����������ʽ��
��2�����õȱ������ε����ʽ��Բ���й����ʵó���AMD=��CMD=$\frac{1}{2}$��AMC=60�㣬�����ó�DC=CM=MA=AD�����ɵó��𰸣�
��3�����ȱ�ʾ����ABP������������n��ֵ���ٴ��뺯����ϵʽ���P�����꣮
��� 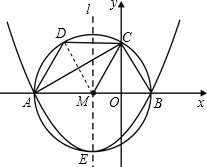 ��1���⣺�������֪����MBCΪ�ȱ������Σ���A��B��C��E���ڡ�M�ϣ�
��1���⣺�������֪����MBCΪ�ȱ������Σ���A��B��C��E���ڡ�M�ϣ�
��MA=MB=MC=ME=2��
�֡�CO��MB��
��MO=BO=1��
��A��-3��0����B��1��0����E��-1��-2����
�����߶���E������Ϊ��-1��-2����
�躯������ʽΪy=a��x+1��2-2��a��0��
�ѵ�B��1��0������y=a��x+1��2-2��
��ã�a=$\frac{1}{2}$��
�ʶ��κ�������ʽΪ��y=$\frac{1}{2}$��x+1��2-2��
��2��֤��������DM��
�ߡ�MBCΪ�ȱ������Σ�
���CMB=60�㣬
���AMC=120�㣬
�ߵ�Dƽ�ֻ�AC��
���AMD=��CMD=$\frac{1}{2}$��AMC=60�㣬
��MD=MC=MA��
���MCD����MDA�ǵȱ������Σ�
��DC=CM=MA=AD��
���ı���AMCDΪ���Σ������߶���ȵ��ı��������Σ���
��3���⣺���ڣ�
�������£�
���P��������m��n��
��S��ABP=$\frac{1}{2}$AB|n|��AB=4
��$\frac{1}{2}$��4��|n|=5��
��2|n|=5��
��ã�n=��$\frac{5}{2}$��
��$n=\frac{5}{2}$ʱ��$\frac{1}{2}$��m+1��2-2=$\frac{5}{2}$��
��˷��̵ã�m1=2��m2=-4
����P��������2��$\frac{5}{2}$������-4��$\frac{5}{2}$����
��n=-$\frac{5}{2}$ʱ��$\frac{1}{2}$��m+1��2-2=-$\frac{5}{2}$��
�˷����⣬
�������P������2��$\frac{5}{2}$������-4��$\frac{5}{2}$����
���� ������Ҫ�����˶��κ����ۺ��Լ����ε��ж�����������������͵ȱ������ε����ʵ�֪ʶ����ȷ�ó�E�������ǽ���ؼ���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | a10-a7=a3 | B�� | ��-2a2b��2=-2a4b2 | C�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D�� | ��a+b��9�£�a+b��3=��a+b��6 |

| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | 4cm | B�� | 2cm | C�� | 4cm��2cm | D�� | 8cm |
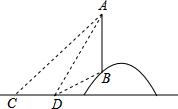 ��ͼ��һ���߸�AB����ɽ���ϣ��ӵ���ĵ�C������ø˶��˵�A������Ϊ45����ǰ��6m�����D���ֲ�ø˶��˵�A�˵˵�B�����Ƿֱ���60���30�㣮
��ͼ��һ���߸�AB����ɽ���ϣ��ӵ���ĵ�C������ø˶��˵�A������Ϊ45����ǰ��6m�����D���ֲ�ø˶��˵�A�˵˵�B�����Ƿֱ���60���30�㣮