题目内容
6.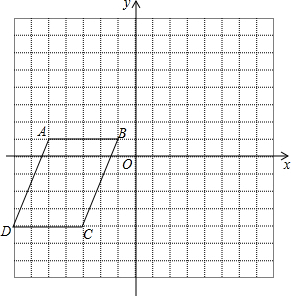 四边形ABCD的顶点坐标分别为A(-5,-1),B(-1,-1),C(-3,-4),D(-7,-4),将四边形ABCD先向上平移5个单位长度,再向右平移8个单位长度.
四边形ABCD的顶点坐标分别为A(-5,-1),B(-1,-1),C(-3,-4),D(-7,-4),将四边形ABCD先向上平移5个单位长度,再向右平移8个单位长度.(1)请直接写出第二次平移后四边形A′B′C′D′各个对应点的坐标和在平面直角坐标系中画出两个四边形.
(2)如果四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移方向和平移距离.
分析 (1)根据图形平移的性质画出四边形A′B′C′D′,并写出各点坐标即可;
(2)根据两四边形的位置即可得出结论.
解答  解:(1)如图所示,由图可知,A′(3,6),B′(7,6),C′(5,1),D′(1,1);
解:(1)如图所示,由图可知,A′(3,6),B′(7,6),C′(5,1),D′(1,1);
(2)∵BB′=$\sqrt{{8}^{2}+{5}^{2}}$=$\sqrt{89}$,
∴四边形A′B′C′D′看成是由四边形ABCD沿BB′的方向平移$\sqrt{89}$个单位.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
16.下列命题是假命题的是( )
| A. | 等角的补角相等 | B. | 内错角相等 | ||
| C. | 两点之间,线段最短 | D. | 同旁内角互补,两直线平行 |
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
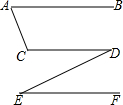 如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.
如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.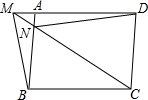 如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.
如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.