��Ŀ����
3��̽���⣺$\sqrt{{3}^{2}}$=3��$\sqrt{0��{5}^{2}}$=0.5��$\sqrt{��-6��^{2}}$=6��$\sqrt{��-\frac{3}{4}��^{2}}$=$\frac{3}{4}$��$\sqrt{{0}^{2}}$=0��
���ݼ��������ش�
��1��$\sqrt{{a}^{2}}$һ������a��������ǣ���ô$\sqrt{{a}^{2}}$=|a|��
��2���������ܽ�Ĺ��ɣ����㣺
����x��2����$\sqrt{��x-2��^{2}}$=2-x��
��$\sqrt{��3.14-��^{2}}$=��-3.14��
��3����a��b��cΪ�����ε����߳�������$\sqrt{��a+b-c��^{2}}$+$\sqrt{��b-c-a��^{2}}$+$\sqrt{��b+c-a��^{2}}$��
���� ���ݶ��θ�ʽ�����ʼ�������𰸣�
��� �⣺$\sqrt{��-6��^{2}}$=$\sqrt{36}$=6��$\sqrt{��-\frac{3}{4}��^{2}}$=$\sqrt{\frac{9}{16}}$=$\frac{3}{4}$��
��1���������֪��$\sqrt{{a}^{2}}$=|a|��
��2���ٵ�x��2ʱ��
��x-2��0��
��$\sqrt{{��x-2��}^{2}}$=|x-2|=-��x-2��=2-x��
�ڡ�3.14-�У�0��
��$\sqrt{{��3.14-��}^{2}}$=|3.14-��|=��-3.14��
��3����a+b��c��b��c+a��b+c��a��
��a+b-c��0��b-c-a��0��b+c-a��0��
��ԭʽ=|a+b-c|+|b-c-a|+|b+c-a|
=a+b-c-��b-c-a��+��b+c-a��
=a+b+c
�ʴ�Ϊ��6��$\frac{3}{4}$
��1��|a|��
��2����2-x���ڦ�-3.4
���� ���⿼����θ�ʽ�����ʣ�����Ĺؼ�����ȷ������Ŀ��������������ӣ��������ڻ������ͣ�

��ϰ��ϵ�д�
 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
�����Ŀ
15�� ��ͼ��һ�������ͼ�������A+��B+��C+��D+��E�Ķ����ǣ�������
��ͼ��һ�������ͼ�������A+��B+��C+��D+��E�Ķ����ǣ�������
 ��ͼ��һ�������ͼ�������A+��B+��C+��D+��E�Ķ����ǣ�������
��ͼ��һ�������ͼ�������A+��B+��C+��D+��E�Ķ����ǣ�������| A�� | 180�� | B�� | 150�� | C�� | 135�� | D�� | 120�� |
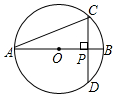 ��ͼ��AB�ǡ�O��ֱ������CD��AB������Ϊ��P����AB=4��AC=2$\sqrt{3}$��
��ͼ��AB�ǡ�O��ֱ������CD��AB������Ϊ��P����AB=4��AC=2$\sqrt{3}$�� ��֪����ͼ���Ծ���ABCD��һ��CDΪ���������ȱߡ�PCD���������̶ȵ�ֱ�������߶�AB�Ĵ�ֱƽ���ߣ�������ͼ�ۼ���
��֪����ͼ���Ծ���ABCD��һ��CDΪ���������ȱߡ�PCD���������̶ȵ�ֱ�������߶�AB�Ĵ�ֱƽ���ߣ�������ͼ�ۼ���
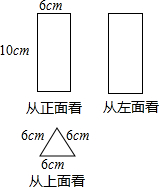 ��ͼ�ǴӲ�ͬ����һ��������õ�����״ͼ���������ݣ�
��ͼ�ǴӲ�ͬ����һ��������õ�����״ͼ���������ݣ�