题目内容
4.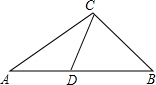 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )| A. | ∠ABC=∠ACD | B. | $\frac{BC}{AC}$=$\frac{CD}{AD}$ | C. | $\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$ | D. | ∠A=∠BCD |
分析 由AC2=AD•AB,得到$\frac{AC}{AB}=\frac{AD}{AC}$,推出△ACD∽△ABC,根据相似三角形的性质即可得到结论.
解答 解:∵AC2=AD•AB,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∵∠A是公共角,
∴△ACD∽△ABC,
∴∠ABC=∠ACD,故A选项正确,$\frac{BC}{AC}=\frac{CD}{AD}$,故B选项正确,
∴$\frac{BC}{CD}=\frac{AC}{AD}$,
∴$\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{A{C}^{2}}{A{D}^{2}}$,
∵AC2=AB•AD,
∴$\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$,故C选项正确,
故选D.
点评 本题考查的是相似三角形的判定和性质,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
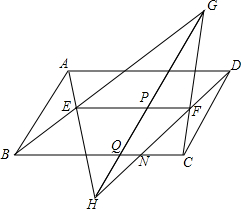 如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.
如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.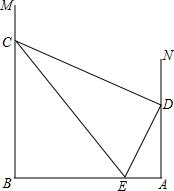 如图,过线段AB两端点分别作MB⊥AB,NA⊥AB,垂足分别为点B、点A;点D是射线AN上的-点,点E是线段AB上的一动点,联结DE,过点D作DC⊥DE,与射线BM交于点C,联结CE;
如图,过线段AB两端点分别作MB⊥AB,NA⊥AB,垂足分别为点B、点A;点D是射线AN上的-点,点E是线段AB上的一动点,联结DE,过点D作DC⊥DE,与射线BM交于点C,联结CE; 如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.
如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.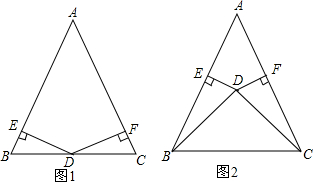
 一个由若干个小正方体搭建而成的几何体的三视图如图,则搭建这个几何体的小正方体有8个.
一个由若干个小正方体搭建而成的几何体的三视图如图,则搭建这个几何体的小正方体有8个.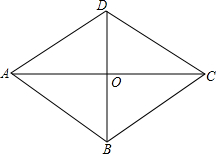 如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:
如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒: