题目内容
9.(1)如图,已知在△ABC中,D在BC上,DB=DC,DE⊥AB,DF⊥AC,且DE=DF,求证:AB=AC;(2)若把条件“D在BC上”点改成“D在△ABC内部”,其他条件不变,结论还成立吗?若成立,给出证明过程;若不成立,也请说明理由.
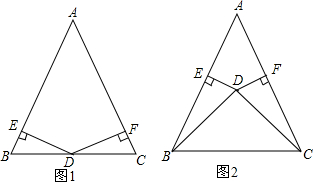
分析 (1)利用HL证明Rt△BED与Rt△DFC全等,进而得出∠B=∠C,利用等角对等边证明即可;
(2)利用HL证明Rt△BED与Rt△DFC全等,进而得出∠EBD=∠FCD,进而得出∠ABC=∠ACB,利用等角对等边证明即可.
解答 证明:(1)∵DB=DC,DE⊥AB,DF⊥AC,且DE=DF,
在Rt△BED与Rt△DFC中,
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$
∴Rt△BED≌Rt△DFC(HL),
∴∠B=∠C,
∴AB=AC;
(2)成立,理由如下:
∵DB=DC,DE⊥AB,DF⊥AC,且DE=DF,
在Rt△BED与Rt△DFC中,
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$
∴Rt△BED≌Rt△DFC(HL),
∴∠EBD=∠FCD,
∵DB=DC,
∴∠DBC=∠DCB,
∴∠ABC=∠ACB,
∴AB=AC.
点评 此题考查全等三角形的判定和性质,关键是利用HL证明Rt△BED与Rt△DFC全等.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4. 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )| A. | ∠ABC=∠ACD | B. | $\frac{BC}{AC}$=$\frac{CD}{AD}$ | C. | $\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$ | D. | ∠A=∠BCD |
19.若a>0,b<0,那么a-b的值( )
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 不能确定 |
 如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积.
如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积.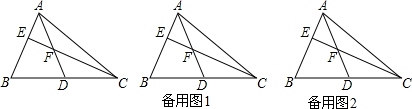
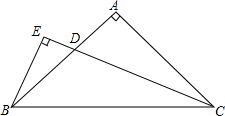 如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.
如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.