题目内容
14.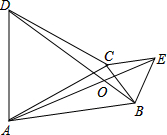 如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为120°.
如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为120°.
分析 先证明∴△DCB≌△ACE,再利用“8字型”证明∠AOH=∠DCH=60°即可解决问题.
解答 解:如图:AC与BD交于点H.
∵△ACD,△BCE都是等边三角形,
∴CD=CA,CB=CE,∠ACD=∠BCE=60°,
∴∠DCB=∠ACE,
在△DCB和△ACE中,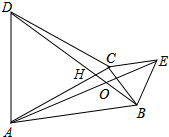
$\left\{\begin{array}{l}{CD=CA}\\{∠DCB=∠ACE}\\{CB=CE}\end{array}\right.$,
∴△DCB≌△ACE,
∴∠CAE=∠CDB,
∵∠DCH+∠CHD+∠BDC=180°,∠AOH+∠AHO+∠CAE=180°,∠DHC=∠OHA,
∴∠AOH=∠DCH=60°,
∴∠AOB=180°-∠AOH=120°.
故答案为120°
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.解分式方程$\frac{1}{x-1}+1=0$,正确的结果是( )
| A. | x=0 | B. | x=1 | C. | x=2 | D. | 无解 |
19.已知命题“关于x的一元二次方程x2+bx+1=0,必有实数解”是假命题,则在下列选项中,b的值可以是( )
| A. | b=-3 | B. | b=-2 | C. | b=-1 | D. | b=2 |
6.如果关于x的一元二次方程x2-6x+2k=0有两个实数根,那么实数k的取值范围是( )
| A. | $k≤\frac{9}{2}$ | B. | $k<\frac{9}{2}$ | C. | $k≥\frac{9}{2}$ | D. | $k>\frac{9}{2}$ |
3.下列运算正确的是( )
| A. | m6÷m2=m3 | B. | 3m2-2m2=m2 | C. | (3m2)3=9m6 | D. | $\frac{1}{2}$m•2m2=m2 |
 如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12,
如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12, 如图,在矩形ABCD中,AB=5,BC=10$\sqrt{3}$,一圆弧过点B和点C,且与AD相切,则图中阴影部分面积为75$\sqrt{3}$-$\frac{100π}{3}$.
如图,在矩形ABCD中,AB=5,BC=10$\sqrt{3}$,一圆弧过点B和点C,且与AD相切,则图中阴影部分面积为75$\sqrt{3}$-$\frac{100π}{3}$.