题目内容
8.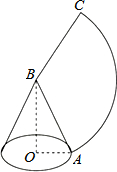 如图,将Rt△AOB绕直角边OB所在的直线旋转一周,得到的旋转体的侧面展开图的圆心角度数为120°,若OB=4$\sqrt{2}$cm,则该旋转体的表面积为( )
如图,将Rt△AOB绕直角边OB所在的直线旋转一周,得到的旋转体的侧面展开图的圆心角度数为120°,若OB=4$\sqrt{2}$cm,则该旋转体的表面积为( )| A. | 16πcm2 | B. | 12πcm2 | C. | 18πcm2 | D. | 12$\sqrt{2}$πcm2 |
分析 设圆锥的底面半径为OA=rcm,得出底面周长为2πrcm,进一步计算展开后算得弧长AC=$\frac{120π•AC}{360}$,建立方程求得AC=3r,进一步利用勾股定理求得r,利用扇形面积计算方法求得答案即可.
解答 解:设圆锥的底面半径为OA=rcm,由题意得
2πr=$\frac{120π•AC}{360}$,
AC=3r,
由勾股定理得
(3r)2-r2=(4$\sqrt{2}$)2
解得:r=2,
因此该旋转体的表面积为$\frac{120π×{6}^{2}}{360}$+π×22=16π.
故选:A.
点评 此题考查圆锥的表面积计算,勾股定理的运用,利用底面圆的周长与展开后的弧长相等得出底面半径和母线的关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
17.形如ax2+bx+c=0的方程是否是一元二次方程的一般形式,下列说法正确的是( )
| A. | a是任意实数 | B. | 与b,c的值有关 | C. | 与a的值有关 | D. | 与a的符号有关 |
18.下列方程中有两个相等实数根的是( )
| A. | 7x2-x-1=0 | B. | 9x2=4(3x-1) | C. | x2+7x+15=0 | D. | 2x2-$\sqrt{3}$x-2=0 |
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4.B为线段OA的中点.直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合).PQ∥y轴与抛物线交于点Q.
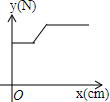
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4.B为线段OA的中点.直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合).PQ∥y轴与抛物线交于点Q.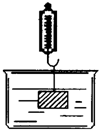 如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )
如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )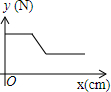
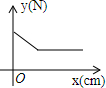
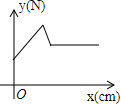
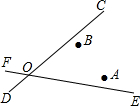 如图,直线CD、EF相交于O,求一点P,使P到直线CD、EF的距离相等,且到A、B两点的距离相等(先说出点的位置,尺规作图,不写作法,保留作图痕迹).
如图,直线CD、EF相交于O,求一点P,使P到直线CD、EF的距离相等,且到A、B两点的距离相等(先说出点的位置,尺规作图,不写作法,保留作图痕迹).