题目内容
5.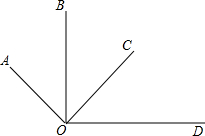 如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC中,正确的有①③④(填序号).
如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC中,正确的有①③④(填序号).
分析 根据垂直的定义和同角的余角相等分别计算,然后对各小题分析判断即可得解.
解答 解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠AOB+∠COD不一定等于90°,故②错误;
∠BOC+∠AOD=90°-∠AOB+90°+∠AOB=180°,故③正确;
∠AOC-∠COD=∠AOC-∠AOB=∠BOC,故④正确;
综上所述,说法正确的是①③④.
故答案为:①③④.
点评 本题考查了余角和补角,垂直的定义,是基础题,熟记概念与性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
16.已知直角三角形的一直角边长为$\sqrt{5}$,斜边上的高为$\sqrt{3}$,则这个直角三角形的斜边长为( )
| A. | 5$\sqrt{2}$ | B. | 5$\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
10.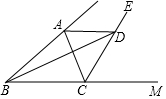 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )| A. | m-a>b-n | B. | m-a<b-n | ||
| C. | m-a=b-n | D. | m-a>b-n或m-a<b-n |
15.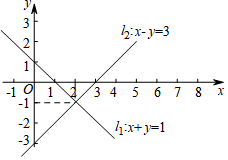 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
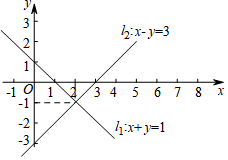 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
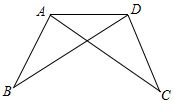 如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.
如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.