题目内容
16．计算：（m2+mn+n2）2-（m2-mn+n2）2．分析 原式利用平方差公式变形，整理即可得到结果．
解答 解：原式=（m2+mn+n2+m2-mn+n2）（m2+mn+n2-m2+mn-n2）
=4mn（m2+n2）．
点评 此题考查了因式分解-运用公式法，熟练掌握平方差公式是解本题的关键．
练习册系列答案
相关题目
7．
如图，在平面直角坐标系中，直线CD与x轴、y轴分别交于点C，D，与反比例函数y=$\frac{k}{x}$（k为常数，且k＞0）在第一象限的图象交于E，F．过点E作EA⊥y轴于A，过点F作FB⊥x轴于B，直线EA与FB交于点G．若$\frac{DE}{DF}$=$\frac{1}{4}$，记△GEF的面积为S1，△OEF的面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）
如图，在平面直角坐标系中，直线CD与x轴、y轴分别交于点C，D，与反比例函数y=$\frac{k}{x}$（k为常数，且k＞0）在第一象限的图象交于E，F．过点E作EA⊥y轴于A，过点F作FB⊥x轴于B，直线EA与FB交于点G．若$\frac{DE}{DF}$=$\frac{1}{4}$，记△GEF的面积为S1，△OEF的面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{3}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{8}$ |
4．
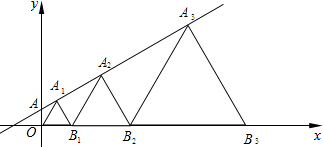如图，在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1，以O、A1为顶点做第一个等边三角形OA1B1，再在直线上取一点A2，以A2、B1为顶点作第二个等边三角形A2B1B2，…，一直这样做下去，则第10个等边三角形的边长为（ ）
如图，在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1，以O、A1为顶点做第一个等边三角形OA1B1，再在直线上取一点A2，以A2、B1为顶点作第二个等边三角形A2B1B2，…，一直这样做下去，则第10个等边三角形的边长为（ ）| A． | （$\frac{\sqrt{3}}{3}$）9 | B． | （$\frac{\sqrt{3}}{3}$）10 | C． | 29•$\sqrt{3}$ | D． | 210•$\sqrt{3}$ |
如图所示，点D、E分别是△ABC边AB、AC上的点，且DE∥BC，BD=3AD，那么△ADE的周长：△ABC的周长=1：4．