题目内容
12.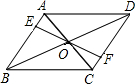 如图,四边形ABCD中,EF过对角线交点,且OB+BE=OD+DF,若OE=OF,证明四边形ABCD为平行四边形.
如图,四边形ABCD中,EF过对角线交点,且OB+BE=OD+DF,若OE=OF,证明四边形ABCD为平行四边形.
分析 延长OB至G,使BG=BE;延长OD至H,使DH=DF;由等腰三角形的性质得出∠1=∠G,∠H=∠2,证出OG=OH,由SAS证明△GOE≌△HOF,得出∠G=∠H,证出∠3=∠4,证出AB∥CD,由AAS证明△BOE≌△DOF,得出BE=DF,同理:AE=CF,得出AB=CD,即可得出结论.
解答 证明:延长OB至G,使BG=BE;延长OD至H,使DH=DF;如图所示: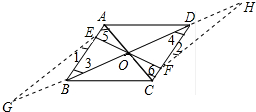 则∠1=∠G,∠H=∠2,
则∠1=∠G,∠H=∠2,
∴∠3=2∠G,∠4=2∠H,
∵OG=OB+BG,OH=OD+DH,OB+BE=OD+DF,
∴OG=OH,
在△GOE和△HOF中,$\left\{\begin{array}{l}{OE=OF}&{\;}\\{∠EOG=∠FOH}&{\;}\\{OG=OH}&{\;}\end{array}\right.$,
∴△GOE≌△HOF(SAS),
∴∠G=∠H,
∴∠3=∠4,
∴AB∥CD,
∴∠5=∠6,
在△BOE和△DOF中,$\left\{\begin{array}{l}{∠3=∠4}&{\;}\\{∠BOE=∠DOF}&{\;}\\{OE=OF}&{\;}\end{array}\right.$,
∴△BOE≌△DOF(AAS),
∴BE=DF,
同理:AE=CF,
∴AB=CD,
∴四边形ABCD为平行四边形.
点评 本题考查了平行四边形的判定方法、全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握平行四边形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7. 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
4.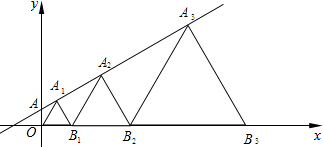 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )| A. | ($\frac{\sqrt{3}}{3}$)9 | B. | ($\frac{\sqrt{3}}{3}$)10 | C. | 29•$\sqrt{3}$ | D. | 210•$\sqrt{3}$ |
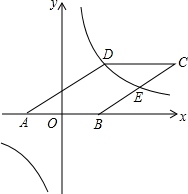 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标. 已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.
已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.