题目内容
6.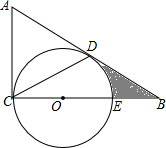 如图,CE是⊙O的直径,AC为⊙0的切线,D为⊙O上的一点,∠A=2∠DCE,延长AD交CE的延长线于点B,连接CD.若BE=OE=2.
如图,CE是⊙O的直径,AC为⊙0的切线,D为⊙O上的一点,∠A=2∠DCE,延长AD交CE的延长线于点B,连接CD.若BE=OE=2.(1)求证:AD为⊙O的切线;
(2)求图中阴影部分的面积(结果保留π)
分析 (1)连接OD,由AD=AC,OD=OC,可得∠ADC=∠ACD,∠ODC=∠OCD,又CA为切线,可知∠ADO=∠ACB=90°,可得AD为切线;
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案.
解答 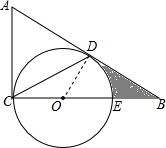 (1)证明:如图,连接OD,
(1)证明:如图,连接OD,
∵AD=AC,
∴∠ADC=∠ACD,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC+∠ODC=∠ACD+∠OCD,
即∠ADO=∠ACB,
∵CE是⊙O的直径,AC是⊙O的切线,
∴BC⊥AC,
∴∠ADO=∠ACB=90°,
∴AD为⊙O的切线;
(2)解:∵∠ODB=90°,OD=2,BO=2+2=4,
由勾股定理得:BD=2$\sqrt{3}$,
∴阴影部分的面积S=S△ODB-S扇形DOE=$\frac{1}{2}$×2$\sqrt{3}$×2-$\frac{60π•{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题主要考查切线的性质和判定及扇形的计算,掌握切线问题中的两种辅助线的作法及扇形的面积公式是解题的关键.

练习册系列答案
相关题目
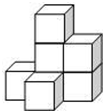 如图,若干个小正方体组成一个几何体.
如图,若干个小正方体组成一个几何体. 如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求:
如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求: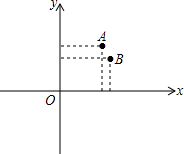 综合平面直角坐标系,探讨:
综合平面直角坐标系,探讨: 如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6.
如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6.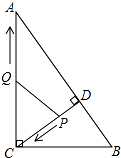 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.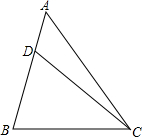 已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.
已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC. 如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由.
如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由.