题目内容
9.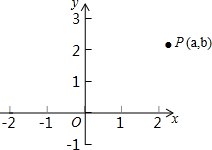 如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点.
如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点.(1)若$a=\sqrt{3}$,$b=\sqrt{6}$,求点P到点O的距离;
(2)若a、b满足$\sqrt{a^2}-{({\sqrt{b}})^2}=0$,且2≤b≤3,求所有的点P组成的图形面积.
分析 (1)根据直角坐标系内的点(x,y)到原点的距离公式即可得到结果;
(2)由二次根式的性质化简,得出a、b的关系,再由2≤b≤3得出a的取值范围,进一步得出由动点P得到的图形,求得答案即可.
解答 解:(1)OP=$\sqrt{(\sqrt{3})^{2}+(\sqrt{6})^{2}}$
=$\sqrt{3+6}$
=$\sqrt{9}$
=3;
(2)∵$\sqrt{a^2}-{({\sqrt{b}})^2}=0$,
∴|a|-b=0,
∴|a|=b,
∵2≤b≤3,
∴2≤|a|≤3,
∴-3≤a≤-2,或2≤a≤3,
∴所有的点P组成的图形是两个边长为1的正方形,如图,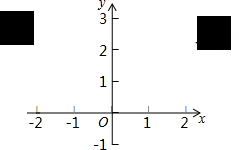
面积为2.
点评 本题考查的是勾股定理,坐标与图形性质,解答本题的关键是解答本题的关键是熟练掌握直角坐标系内的点(x,y)到原点的距离公式d=$\sqrt{{x}^{2}+{y}^{2}}$.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
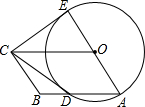 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线, 如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求:
如图,将边长为8的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,求: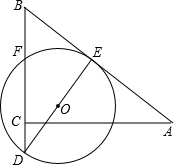 如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.
如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A. 综合平面直角坐标系,探讨:
综合平面直角坐标系,探讨: 如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6.
如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6. 已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.
已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.