题目内容
 已知,如图,AC⊥BF于点C,DF⊥AB于点D,且D是AB的中点.求证:CD2=DE•DF.
已知,如图,AC⊥BF于点C,DF⊥AB于点D,且D是AB的中点.求证:CD2=DE•DF.考点:相似三角形的判定与性质
专题:证明题
分析:AC⊥BF,DF⊥AB则可知∠A+∠B=∠F+∠B=90°,所以∠A=∠F,且∠ADE=∠BDF=90°,所以△ADE∽△FDB,所以
=
,且D为AB的中点,所以CD=AD=BD,代入结论可证.
| AD |
| DF |
| DE |
| BD |
解答:证明:∵AC⊥BF,DF⊥AB,
∴∠A+∠B=∠F+∠B=90°,
∴∠ADE=∠BDF=90°,
∴△ADE∽△FDB,
∴
=
,
且D为AB的中点,
∴CD=AD=BD,
∴CD2=DE•DF.
∴∠A+∠B=∠F+∠B=90°,
∴∠ADE=∠BDF=90°,
∴△ADE∽△FDB,
∴
| AD |
| DF |
| DE |
| BD |
且D为AB的中点,
∴CD=AD=BD,
∴CD2=DE•DF.
点评:本题主要考查三角形相似的判定和性质,解题的关键是证明△ADE∽△FDB.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
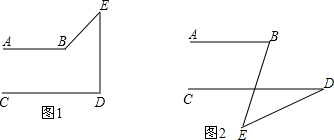 猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.
猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明. 如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.
如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.