题目内容
 已知:如图,E是AD上一点,∠1=∠2,∠3=∠4;
已知:如图,E是AD上一点,∠1=∠2,∠3=∠4;求证:(1)AB=AC;(2)DB=DC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)如图,直接运用ASA公理证明△ABE≌△ACE,得到AB=AC即可解决问题.
(2)运用ASA公理证明△ABD≌△ACD,即可解决问题.
(2)运用ASA公理证明△ABD≌△ACD,即可解决问题.
解答: 解:(1)证明:在△ABE与△ACE中,
解:(1)证明:在△ABE与△ACE中,
,
∴△ABE≌△ACE(ASA),
∴AB=AC.
(2)在△ABD与△ACD中,
,
∴△ABD≌△ACD,
∴DB=DC.
 解:(1)证明:在△ABE与△ACE中,
解:(1)证明:在△ABE与△ACE中,
|
∴△ABE≌△ACE(ASA),
∴AB=AC.
(2)在△ABD与△ACD中,
|
∴△ABD≌△ACD,
∴DB=DC.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;牢固掌握全等三角形的判定及其性质是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
下列运算正确的是( )
| A、(-a2)3=-a6 |
| B、(a-b)2=a2-b2 |
| C、x2+x2=x4 |
| D、3a2•2a2=6a6 |
已知点A(2,-2),如果把点A向上平移4个单位,再向左平移4个单位得到点C,那么C点的坐标是( )
| A、(-2,2) |
| B、(2,2) |
| C、(-1,-1) |
| D、(-2,-2) |
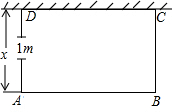 某学校农场要盖一间长方形牛棚,打算一面用一堵旧墙(墙长10米),其余各面用19米长木料围成栅栏,AD边留有1米宽的门.设与墙垂直的栅栏AD长x米,
某学校农场要盖一间长方形牛棚,打算一面用一堵旧墙(墙长10米),其余各面用19米长木料围成栅栏,AD边留有1米宽的门.设与墙垂直的栅栏AD长x米, 如图,将4个直角边长为1和
如图,将4个直角边长为1和