题目内容
 如图,将4个直角边长为1和
如图,将4个直角边长为1和| 3 |
考点:勾股定理
专题:
分析:先根据勾股定理求出斜边的长,再根据正方形的面积公式即可得出正方形ABCD的面积;再利用正方形ABCD的面积-三角形的面积即可得出正方形EFGH的面积.
解答:解:∵直角三角形的直角边分别为1,
,
∴斜边=
=2,
∴S正方形ABCD=2×2=4,
S正方形EFGH=S正方形ABCD-4S△ABF=4-4×
×1×
=4-2
.
| 3 |
∴斜边=
12+(
|
∴S正方形ABCD=2×2=4,
S正方形EFGH=S正方形ABCD-4S△ABF=4-4×
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要
用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要 已知:如图,E是AD上一点,∠1=∠2,∠3=∠4;
已知:如图,E是AD上一点,∠1=∠2,∠3=∠4;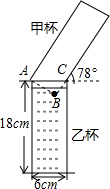 如图,有两个高度相等且底面直径不等的圆柱形水杯,中杯转满液体,乙杯是空杯,若把甲杯中的液体全部倒人乙杯,则乙杯中的液面与图中点B的距离约为多少?(结果精确到0.01cm,参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
如图,有两个高度相等且底面直径不等的圆柱形水杯,中杯转满液体,乙杯是空杯,若把甲杯中的液体全部倒人乙杯,则乙杯中的液面与图中点B的距离约为多少?(结果精确到0.01cm,参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)