题目内容
9.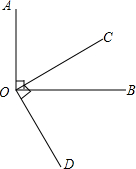 如图,OA⊥OB于点O,OC⊥OD于点O,求证:∠AOC=∠BOD(要求写出每一步推理的依据)
如图,OA⊥OB于点O,OC⊥OD于点O,求证:∠AOC=∠BOD(要求写出每一步推理的依据)
分析 根据垂直的定义可得出∠AOB=90°、∠COD=90°,即∠AOC+∠BOC=∠BOD+∠BOC,由此即可证出∠AOC=∠BOD.
解答  证明:∵OA⊥OB于点O(已知),
证明:∵OA⊥OB于点O(已知),
∴∠AOB=90°(垂直定义),
∴∠AOC+∠BOC=90°(等量代换).
∵OC⊥OD于点O(已知),
∴∠COD=90°(垂直定义),
∴∠BOD+∠BOC=90°(等量代换),
∴∠AOC=∠BOD(同角的余角相等).
点评 本题考查了垂线以及余角和补角,根据同角的余角相等找出∠AOC=∠BOD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列各组的运算结果相等的是( )
| A. | 34和43 | B. | -($\frac{1}{2}$)3和(-$\frac{1}{2}$)3 | C. | -22和 (-2 )2 | D. | |-3|和-|-3| |
 已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=36cm2,则△DEC的面积为9cm2.
已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=36cm2,则△DEC的面积为9cm2.
 如图,∠ABC=∠ADC=90°,AB=AD,AC,BD相交于点O,求证:OD=OB.
如图,∠ABC=∠ADC=90°,AB=AD,AC,BD相交于点O,求证:OD=OB.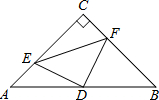 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF. 已知:如图,AB=CD,AD=BC.求证:AB∥CD.
已知:如图,AB=CD,AD=BC.求证:AB∥CD.