题目内容
16. 甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
分析 根据甲到达B地后用半小时办完事求出b=1+$\frac{1}{2}$=$\frac{3}{2}$,由图可知乙的速度为(6-4)÷$\frac{1}{2}$=4(千米/小时),则甲的速度为6+4=10(千米/小时),则4千米两人相遇所用时间为4÷(4+10)=$\frac{2}{7}$,所以a=b+$\frac{2}{7}$,即可解答.
解答 解:如图,
∵到达B地后用半小时办完事,
∴b=1+$\frac{1}{2}$=$\frac{3}{2}$,
由图可知乙的速度为(6-4)÷$\frac{1}{2}$=4(千米/小时),则甲的速度为6+4=10(千米/小时),
则4千米两人相遇所用时间为4÷(4+10)=$\frac{2}{7}$,
所以a=b+$\frac{2}{7}$=$\frac{3}{2}+\frac{2}{7}=\frac{25}{14}$.
点评 本题考查了一次函数的应用,主要利用了路程、速度、时间三者之间的关系,读懂题目信息,理解甲乙二人的行驶过程是解题的关键.

练习册系列答案
相关题目
4.下列二元一次方程组中,以$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$为解的是( )
| A. | $\left\{\begin{array}{l}x-y=1\\ 3x+y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-2y=-3\\ 3x+y=5\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-y=1\\ 3x+y=-5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=3\\ 3x+y=4\end{array}\right.$ |
 有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,-3)可认,而主要建筑C(3,2)破损,试通过建立直角坐标系找到图中C点的位置后,则线段AC的长$\sqrt{37}$.
有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,-3)可认,而主要建筑C(3,2)破损,试通过建立直角坐标系找到图中C点的位置后,则线段AC的长$\sqrt{37}$.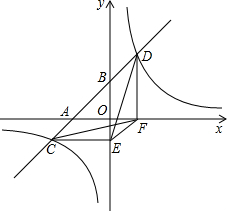 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论: