题目内容
11.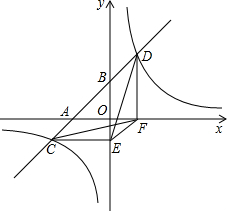 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:①S△CEF=S△DEF;②△AOB相似于△FOE;③△DCE≌△CDF;④AC=BD
其中正确的结论是①②④.(把你认为正确结论的序号都填上)
分析 设D(x,$\frac{k}{x}$),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据相似三角形的判定判断②即可;根据全等三角形的判定判断③即可;证出平行四边形BDFE和平行四边形ACEF,可推出AC=BD,判断④即可.
解答  解:①设D(x,$\frac{k}{x}$),则F(x,0),
解:①设D(x,$\frac{k}{x}$),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是:$\frac{1}{2}$×$\frac{k}{x}$×x=$\frac{1}{2}$k,
设C(a,$\frac{k}{a}$),则E(0,$\frac{k}{a}$),
由图象可知:a>0,$\frac{k}{a}$<0,
△CEF的面积是:$\frac{1}{2}$×|a|×|$\frac{k}{a}$|=$\frac{1}{2}$|k|,
∴△CEF的面积=△DEF的面积,
故①正确;
②△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
∴EF∥CD,
∴FE∥AB,
∴△AOB∽△FOE,
故②正确;
③BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BE=DF,而只有当a=1时,才有CE=BE,
即CE不一定等于DF,故△DCE≌△CDF不一定成立;
故③错误;
④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
故④正确;
正确的有3个:①②④.
故答案为:①②④.
点评 本题考查了反比例函数综合题,三角形的面积,全等三角形的判定,相似三角形的判定,检查同学们综合运用定理进行推理的能力,关键是需要同学们牢固掌握课本知识.

练习册系列答案
相关题目
2.已知在半径分别为4cm和7cm的两圆相交,则它们的圆心距可能是( )
| A. | 1cm | B. | 3cm | C. | 10cm | D. | 15cm |
 在直角坐标系xOy中,直线l过(1,3)和(2,1)两点,且与x轴,y轴分别交于A,B两点.
在直角坐标系xOy中,直线l过(1,3)和(2,1)两点,且与x轴,y轴分别交于A,B两点. 如图所示,共有直线2条,射线7条,线段6条.
如图所示,共有直线2条,射线7条,线段6条. 甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
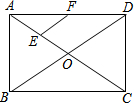 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.