题目内容
5.在Rt△ABC中,AB=c,BC=a,AC=b,∠B=90°.(1)已知b=8,c=4,求a.
(2)已知b=$\sqrt{5}$,a:c=1:2,求a、c.
分析 (1)由题意可知:斜边为b,直角边为a、c,直接由勾股定理求得答案即可;
(2)由a:c=1:2,得出c=2a,利用勾股定理求得答案即可.
解答 解:(1)a=$\sqrt{{b}^{2}-{c}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$;
(2)∵a:c=1:2,
∴c=2a,
∵a2+c2=b2,
∴5a2=b2,
∵b=$\sqrt{5}$,
∴a=1,则c=2.
点评 本题考查了勾股定理在直角三角形中的运用,掌握勾股定理是解决问题的关键.

练习册系列答案
相关题目
15.下表是某校七、八年级某月课外兴趣小组活动时间统计表,其中各年级文艺小组每次活动时间为2h;各年级科技小组每次活动时间为1.5h.
(1)若七年级科技小组活动次数比文艺小组活动次数少一次,请你用一元一次方程知识求七年级科技小组与文艺小组的活动次数分别为多少?
(2)请你利用表格信息,直接写出八年级科技小组活动次数为4次.
| 课外小组活动总时间/h | 文艺小组活动次数 | 科技小组活动次数 | |
| 七年级 | 12.5 | ||
| 八年级 | 12 | 3 |
(2)请你利用表格信息,直接写出八年级科技小组活动次数为4次.
17. 如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
 如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )| A. | 19° | B. | 71° | C. | 109° | D. | 119° |
15.下列式子中计算正确的是( )
| A. | 5xy2-5y2x=0 | B. | 5a2-2a2=3 | C. | 4x2y-xy2=3xy2 | D. | 2a+3b=5ab |
 甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
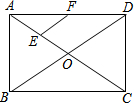 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm. 如图,△ABC中,点D、E、F分别是AB、BC、AC的中点,则与△ADF位似的三角形是△ABC.
如图,△ABC中,点D、E、F分别是AB、BC、AC的中点,则与△ADF位似的三角形是△ABC.