题目内容
8.如图,矩形CDEF代表建筑物,身高1.65米的兵兵在建筑物前点B处放风筝,风筝不小心挂在树枝点G处(在FE的延长线上).经测量,兵兵距建筑物BC=5米,建筑物底部宽FC=7米,并且点G、D、A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,若兵兵充分利用梯子和一根5米长的竹竿能否触到挂在树上的风筝?

分析 (1)过A作AP⊥GF于点P,如图,利用矩形的性质得AP=BF=CF+BC=12,AB=PF=1.4,再在Rt△PAG中,根据正切的定义可计算出GP=AP•tan37°=9(米),于是得到GF=GP+PF≈10.4(米);
(2)在直角△MNF中,利用勾股定理计算出NF=4,然后通过比较梯子、竹竿和身高的和与挂在树上的风筝的高度的大小进行判断.
解答 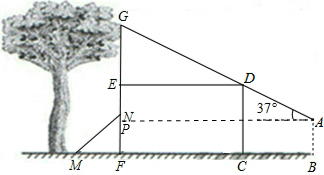 解:(1)过A作AP⊥GF于点P,如图,则AP=BF=CF+BC=7+5=12,AB=PF=1.4,∠GAP=37°,
解:(1)过A作AP⊥GF于点P,如图,则AP=BF=CF+BC=7+5=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中,tan∠PAG=$\frac{GP}{AP}$,
∴GP=AP•tan37°≈12×0.75=9(米),
∴GF=GP+PF=9+1.4≈10.4(米);
(2)由题意可知MN=5,MF=3,
在直角△MNF中,NF=$\sqrt{M{N}^{2}-M{F}^{2}}$=4,
∵4+1.65+5=10.65,
10.65>10.4,
即梯子、竹竿和身高的和大于挂在树上的风筝的高度,
∴兵兵充分利用梯子和一根5米长的竹竿能触到挂在树上的风筝.
点评 本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
相关题目
17. 如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
 如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )
如图,已知∠1=∠2,∠3=71°,则∠4的度数是( )| A. | 19° | B. | 71° | C. | 109° | D. | 119° |
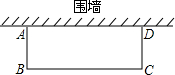 如图,利用已有的围墙对邻边不等的矩形花圃ABCD修建栅栏,已知三边所围的栅栏的总长度是6m,且可利用的围墙长度超过6m,若矩形ABCD的面积为4m2,试求边AB的长度.
如图,利用已有的围墙对邻边不等的矩形花圃ABCD修建栅栏,已知三边所围的栅栏的总长度是6m,且可利用的围墙长度超过6m,若矩形ABCD的面积为4m2,试求边AB的长度. 如图所示,共有直线2条,射线7条,线段6条.
如图所示,共有直线2条,射线7条,线段6条. 甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.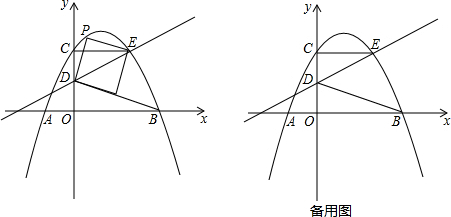

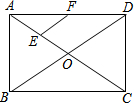 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.