题目内容
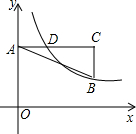 如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y=
如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y=| k |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:先设B(3,a),则D(1,a+2),再根据反比例函数y=
(x>0)的图象经过点B,D得出3a=a+2,求出a的值,进而得出B点坐标,求出k的值即可.
| k |
| x |
解答:解:∵点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,
∴设B(3,a),则D(1,a+2),
∵反比例函数y=
(x>0)的图象经过点B,D,
∴3a=a+2,解得a=1,
∴B(3,1),
∴k=3×1=3.
故答案为:3.
∴设B(3,a),则D(1,a+2),
∵反比例函数y=
| k |
| x |
∴3a=a+2,解得a=1,
∴B(3,1),
∴k=3×1=3.
故答案为:3.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、3x3-5x3=-2 |
| B、(6x3)÷(2x2)=3x(x≠0) |
| C、(x3)2=x5 |
| D、-3x(2x-4)=-6x2-12x |
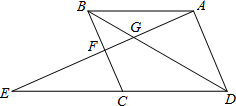 如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.
如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长. 如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为
如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为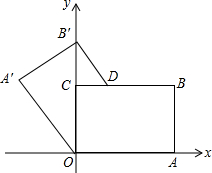 如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为
如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为