题目内容
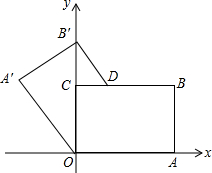 如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为
如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为考点:翻折变换(折叠问题),反比例函数图象上点的坐标特征
专题:计算题
分析:作A′E⊥y轴于E,连接OB,如图,在Rt△OAB中,利用勾股定理计算出OB=10,再根据折叠的性质得A′B′=AB=6,OA′=OA=8,OB′=OB=10,∠OA′B′=∠OAB=90°,利用面积法得到A′E=
,在Rt△OA′E中,根据勾股定理计算出OE=
,则A′点的坐标为(-
,
),设经过点A′的反比例函数的解析式为y=
,利用反比例函数图形上点的坐标特征计算出k的值,从而得到经过点A′的反比例函数的解析式.
| 24 |
| 5 |
| 32 |
| 5 |
| 24 |
| 5 |
| 32 |
| 5 |
| k |
| x |
解答: 解:作A′E⊥y轴于E,连接OB,如图,
解:作A′E⊥y轴于E,连接OB,如图,
∵四边形OABC为矩形,
∴AB=OC=6,
在Rt△OAB中,OA=8,
∴OB=
=10,
∵四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上,
∴A′B′=AB=6,OA′=OA=8,OB′=OB=10,∠OA′B′=∠OAB=90°,
∵S△OA′B′=
OA′•A′B′=
OB′•A′E,
∴A′E=
=
,
在Rt△OA′E中,OE=
=
,
∴A′点的坐标为(-
,
),
设经过点A′的反比例函数的解析式为y=
,
∴k=-
×
=-
,
∴经过点A′的反比例函数的解析式为y=-
.
故答案为y=-
.
 解:作A′E⊥y轴于E,连接OB,如图,
解:作A′E⊥y轴于E,连接OB,如图,∵四边形OABC为矩形,
∴AB=OC=6,
在Rt△OAB中,OA=8,
∴OB=
| OA2+AB2 |
∵四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上,
∴A′B′=AB=6,OA′=OA=8,OB′=OB=10,∠OA′B′=∠OAB=90°,
∵S△OA′B′=
| 1 |
| 2 |
| 1 |
| 2 |
∴A′E=
| 6×8 |
| 10 |
| 24 |
| 5 |
在Rt△OA′E中,OE=
| OA′2-A′E2 |
| 32 |
| 5 |
∴A′点的坐标为(-
| 24 |
| 5 |
| 32 |
| 5 |
设经过点A′的反比例函数的解析式为y=
| k |
| x |
∴k=-
| 24 |
| 5 |
| 32 |
| 5 |
| 768 |
| 25 |
∴经过点A′的反比例函数的解析式为y=-
| 768 |
| 25x |
故答案为y=-
| 768 |
| 25x |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了反比例函数图形上点的坐标特征和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列调查中,适合用普查方法的是( )
| A、了解我市所有居民的年收入 |
| B、了解我市居民的环保意识 |
| C、了解我市每天进出的人数 |
| D、了解你校数学教师的年龄状况 |
下列各式能用平方差公式计算的是( )
| A、(2a+b)(2b-a) |
| B、(x+1)(-x-1) |
| C、(-m-n)(-m+n) |
| D、(3x-y)(-3x+y) |
下列数中,绝对值最大的是( )
A、
| ||
| B、0 | ||
| C、-2 | ||
| D、-1 |
 如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于点E,AD=BD.则∠B等于
如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于点E,AD=BD.则∠B等于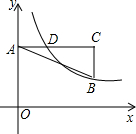 如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y=
如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y= 如图,把一张长方形纸片ABCD沿EF折叠后,ED交BC于点G,点D、C分别落在D′、C′位置上,若∠EFC′=130°,那么∠AEG=
如图,把一张长方形纸片ABCD沿EF折叠后,ED交BC于点G,点D、C分别落在D′、C′位置上,若∠EFC′=130°,那么∠AEG=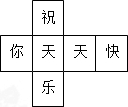 一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( )
一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( )