题目内容
9.先化简,再求值:(2a+b)2-(3a-b)2+5a(a-b),其中$a=\frac{1}{2}$,$b=\frac{1}{5}$.分析 先将整式按完全平方公式和单项式乘多项式展开,再去括号,合并同类项,代入求值即可.
解答 解:原式=4a2+4ab+b2-(9a2-6ab+b2)+5a2-5ab
=4a2+4ab+b2-9a2+6ab-b2+5a2-5ab
=5ab,
当$a=\frac{1}{2}$,$b=\frac{1}{5}$时,
原式=5ab=5×$\frac{1}{2}$×$\frac{1}{5}$=$\frac{1}{2}$.
点评 本题主要考查整式化简求值,熟练掌握完全平方公式及整式的乘法是关键,代入求值是基础.

练习册系列答案
相关题目
20.数据:2,-1,3,5,6,5的众数是( )
| A. | -1 | B. | 4 | C. | 5 | D. | 6 |
17.在函数y=$\frac{{-{k^2}-1}}{x}$(k为常数)的图象上有三个点(x1,-2),(x2,-1),(x3,3),则x1,x2,x3的大小关系为( )
| A. | x1<x2<x3 | B. | x3<x1<x2 | C. | x3<x2<x1 | D. | x2<x1<x3 |
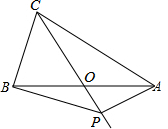 如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.
如图,在△ABC中,AB=AC=4,AO=BO,P是射线CO上的一个动点,∠AOC=120°,则当△PAB为直角三角形时,AP的长为2或2$\sqrt{3}$.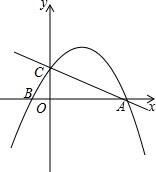 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.