Question

9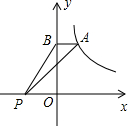．如图，A是反比例函数图象上的一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为4，则这个反比例函数的关系式为y=$\frac{8}{x}$．

Answer 1

分析 由于同底等高的两个三角形面积相等，所以△AOB的面积=△ABP的面积=4，然后根据反比例函数y=$\frac{k}{x}$中k的几何意义，知△AOB的面积=$\frac{1}{2}$|k|，从而确定k的值，求出反比例函数的解析式．

解答 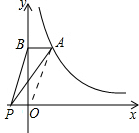解：设反比例函数的解析式为y=$\frac{k}{x}$．
∵△AOB的面积=△ABP的面积=4，△AOB的面积=$\frac{1}{2}$|k|，
∴$\frac{1}{2}$|k|=4，
∴k=±8；
又∵反比例函数的图象的一支位于第一象限，
∴k＞0．
∴k=8．
∴这个反比例函数的解析式为y=$\frac{8}{x}$．
故答案为y=$\frac{8}{x}$．

点评 本题主要考查了待定系数法求反比例函数的解析式和反比例函数y=$\frac{k}{x}$中k的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．