题目内容
13.已知直线y=2x+2与x轴、y轴分别交于点A,B.若将直线y=$\frac{1}{2}$x向上平移n个单位长度与线段AB有公共点,则n的取值范围是$\frac{1}{2}≤n≤2$.分析 先根据直线y=2x+2与x轴、y轴分别交于点A,B,求得A(-1,0),B(0,2),再根据当直线y=$\frac{1}{2}$x+n经过点A时,0=-$\frac{1}{2}$+n,即n=$\frac{1}{2}$;当直线y=$\frac{1}{2}$x+n经过点B时,2=0+n,即n=2,即可得到n的取值范围.
解答 解:∵直线y=2x+2与x轴、y轴分别交于点A,B,
∴A(-1,0),B(0,2),
将直线y=$\frac{1}{2}$x向上平移n个单位长度后得到:直线y=$\frac{1}{2}$x+n,
当直线y=$\frac{1}{2}$x+n经过点A时,0=-$\frac{1}{2}$+n,即n=$\frac{1}{2}$,
当直线y=$\frac{1}{2}$x+n经过点B时,2=0+n,即n=2,
又∵直线y=$\frac{1}{2}$x+n与线段AB有公共点,
∴n的取值范围是$\frac{1}{2}≤n≤2$.
故答案为:$\frac{1}{2}≤n≤2$.
点评 本题主要考查了一次函数图象与几何变换,解题时注意:直线y=kx+b向上平移m(m>0)个单位所得直线解析式为y=kx+b+m,直线y=kx+b向下平移m(m>0)个单位所得直线解析式为y=kx+b-m.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.下表是某校排球队员的年龄分布:
则该校女子排球队员的平均年龄为15岁(结果取整数)
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 5 | 2 |
8.下列四组线段中,不能作为直角三角形三条边的是( )
| A. | 3cm,4cm,5cm | B. | 2cm,2cm,2$\sqrt{2}$cm | C. | 2cm,5cm,6cm | D. | 5cm,12cm,13cm |
19.下列语句:①如果两个角是同位角,那么这两个角相等;②如果两条平行线被第三条直线所截,且同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行;其中( )
| A. | ①、②是真命题 | B. | ②、③是真命题 | C. | ①、③是假命题 | D. | 以上结论都错 |
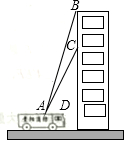 贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).