题目内容
徐晓曼在做练习时,遇到了这样一道习题“当a=
,b=2014时,求多项式3(a2-b2)+4a2b+b2与-3a2-2(2a2b-b2)+2015的和的值”看来这道题,徐晓曼同学犯难的说:“这么大的数字,又有这么复杂的式子,计算太麻烦了”而王晓娟同学却说:“题目中给出的条件是多余的,本题不知道a,b的值照样可以计算”你认为王晓娟的说法有道理吗?为什么?
| 1 |
| 2015 |
考点:整式的加减—化简求值
专题:
分析:先把3(a2+b2)+4a2b+b2与-3a2-2(2a2b-b2)+2015的和进行化简,再判断即可.
解答:解:原式=[3(a2-b2)+4a2b+b2]+[-3a2-2(2a2b-b2)+2015]
=3a2-3b2+4a2b+b2-3a2-4a2b+2b2+2015
=2015,
答:有道理,化简的结果里不含a和b.
=3a2-3b2+4a2b+b2-3a2-4a2b+2b2+2015
=2015,
答:有道理,化简的结果里不含a和b.
点评:本题考查了整式的化简求值,解题的关键是化简求值,把含有a,b的项消去.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
以下列选项中的数为长度的三条线段中,不能组成直角三角形的是( )
| A、8,15,17 |
| B、9,12,15 |
| C、4,6,8 |
| D、7,24,25 |
规定一种新运算“※”,如果a,b是有理数,那么a※b=3a-2b,则2※(-3)=( )
| A、-1 | B、10 | C、12 | D、0 |
 如图所示为利用位似在半圆内作内接正方形,你能分析出作图思路吗?
如图所示为利用位似在半圆内作内接正方形,你能分析出作图思路吗?
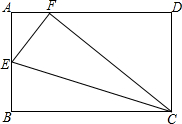 如图所示,小明将一张矩形纸片ABCD,沿CE折叠B点,恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠ECF的值是
如图所示,小明将一张矩形纸片ABCD,沿CE折叠B点,恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠ECF的值是