题目内容
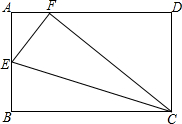 如图所示,小明将一张矩形纸片ABCD,沿CE折叠B点,恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠ECF的值是
如图所示,小明将一张矩形纸片ABCD,沿CE折叠B点,恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠ECF的值是考点:翻折变换(折叠问题)
专题:
分析:先求出DF的长(用λ表示),再求出AF的长;借助勾股定理求出BE的长,进而求出CE的长,即可解决问题.
解答: 解:∵AB:BC=4:5,
解:∵AB:BC=4:5,
∴设AB=4λ,则BC=5λ;
∵四边形ABCD为矩形,
∴∠A=∠B=∠D=90°;
DC=AB=4λ,AD=BC=5λ;
由题意得:CF=BC=5λ,BE=EF(设为μ),
则AE=4λ-μ;由勾股定理得:
DF2=CF2-CD2=25λ2-16λ2,
∴DF=3λ,AF=5λ-3λ=2λ;
由勾股定理得:μ2=(4λ-μ)2+(2λ)2,
解得:μ=
λ;
由勾股定理得:CE2=BE2+BC2
=
+25λ2,
∴CE=
λ,
∴cos∠EFC=
=
=
.
故答案为
.
 解:∵AB:BC=4:5,
解:∵AB:BC=4:5,∴设AB=4λ,则BC=5λ;
∵四边形ABCD为矩形,
∴∠A=∠B=∠D=90°;
DC=AB=4λ,AD=BC=5λ;
由题意得:CF=BC=5λ,BE=EF(设为μ),
则AE=4λ-μ;由勾股定理得:
DF2=CF2-CD2=25λ2-16λ2,
∴DF=3λ,AF=5λ-3λ=2λ;
由勾股定理得:μ2=(4λ-μ)2+(2λ)2,
解得:μ=
| 5 |
| 2 |
由勾股定理得:CE2=BE2+BC2
=
| 25λ2 |
| 4 |
∴CE=
5
| ||
| 2 |
∴cos∠EFC=
| CF |
| CE |
| 5λ | ||||
|
2
| ||
| 5 |
故答案为
2
| ||
| 5 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,AB∥CD,那么∠1+∠2+∠3等于( )
如图,AB∥CD,那么∠1+∠2+∠3等于( )| A、180° | B、360° |
| C、540° | D、720° |
 如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )
如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )| A、11个 | B、12个 |
| C、13个 | D、14个 |
 如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B. 如图所示,已知△ABC和△BDE均为等边三角形,且A、B、E三点共线,连接AD、CE,若∠BAD=39°,那么∠AEC=
如图所示,已知△ABC和△BDE均为等边三角形,且A、B、E三点共线,连接AD、CE,若∠BAD=39°,那么∠AEC=