题目内容
3. 如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.
如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.(1)证明:①△PAB≌△PCB;②△PAF∽△PEA;
(2)若菱形ABCD的边长为3,AP=6,FP=2,求AE的长.
分析 (1)①由菱形的对角线平分对角得出∠ABD=∠CBD,因此∠ABP=∠CBP,再根据SAS即可证明结论;
②先证明∠PFA=∠PAE,再由公共角即可证出结论;
(2)先由△PAF∽△PEA,得出比例式$\frac{PF}{AP}=\frac{AP}{PE}$,求出PE,得出CE、EF,再由平行线得出比例式$\frac{AE}{AD}=\frac{EF}{CF}$,即可求出AE.
解答 (1)证明:①∵四边形ABCD是菱形,
∴AB=CB,∠ABD=∠CBD,
∴∠ABP=∠CBP,
在△PAB和△PCB中,
$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABP=∠CBP}&{\;}\\{BP=BP}&{\;}\end{array}\right.$,
∴△PAB≌△PCB(SAS);
②∵△PAB≌△PCB,∠PAB=∠PCB,
∵四边形ABCD是菱形,
∴∠BAD=∠BCD,DC∥AF,
∴∠PAE=∠PCD,∠PCD=∠PFA,
∴∠PFA=∠PAE,
又∵∠APF=∠EPA,
∴△PAF∽△PEA;
(2)解:∵△PAB≌△PCB,
∴CP=AP=6,
∴CF=6-2=4,
∵△PAF∽△PEA,
∴$\frac{PF}{AP}=\frac{AP}{PE}$,即$\frac{2}{6}=\frac{6}{PE}$,
∴PE=18,
∴CE=18-6=12,EF=16,
∵DC∥AF,
∴$\frac{AE}{AD}=\frac{EF}{CF}$,即$\frac{AE}{3}=\frac{16}{4}$,
∴AE=12.
点评 本题考查了菱形的性质、全等三角形的判定与性质以及相似三角形的判定与性质;证明全等三角形和相似三角形是解决问题的关键.

练习册系列答案
相关题目
12.下列说法不正确的是( )
| A. | $\sqrt{a}$(a≥0)是二次根式 | B. | 当a<0时,($\sqrt{a}$)2=-a | ||
| C. | $\sqrt{{a}^{2}+b}$是最简二次根式 | D. | $\sqrt{(x+3)^{2}}$=x+3成立的条件是x>-3 |
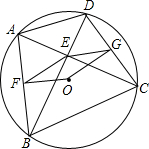 已知:如图,四边形ABCD内接于圆O,其中AC⊥BD,点F和点G分别是线段AB和CD的中点.
已知:如图,四边形ABCD内接于圆O,其中AC⊥BD,点F和点G分别是线段AB和CD的中点.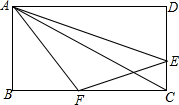 如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似?
如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似?