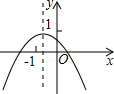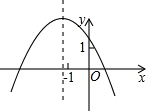题目内容
18.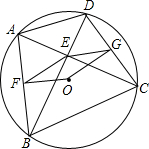 已知:如图,四边形ABCD内接于圆O,其中AC⊥BD,点F和点G分别是线段AB和CD的中点.
已知:如图,四边形ABCD内接于圆O,其中AC⊥BD,点F和点G分别是线段AB和CD的中点.(1)若四边形EFOG为菱形,求证:∠ACB=∠CBD;
(2)求证:四边形EFOG为平行四边形.
分析 (1)利用圆内弦、弦心距以及圆心角之间的关系得出AB=CD,进而得出答案;
(2)利用三角形斜边上中线的性质以及平行线的判定方法结合等腰三角形的性质得出EF∥GO进而得出答案.
解答 证明:(1)∵点F和点G分别是线段AB和CD的中点,
∴OG⊥DC,OF⊥AB,
∵四边形EFOG为菱形,
∴FO=GO,
∴AB=CD,
∴∠ACB=∠CBD;
(2)∵AC⊥DB,
∴∠AEB=∠BEC=∠DEC=90°,
∵点F和点G分别是线段AB和CD的中点,
∴EF=AF=BF,EG=DG=GC,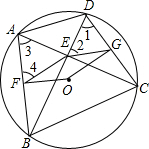
∴∠1=∠2,∠3=∠4,
∵∠2+∠GEC=90°,∠1+∠ACD=90°,
∴∠GEC=∠FEB,
同理可得:∠EGC=∠FEB,
∵∠OGE=90°-∠EGD=90°-(180°-2∠2)=-90°+2∠2,
∠FEG=90°+2(90°-∠2),
∴∠FEG+∠EGO=180°,
∴EF∥GO,
同理可得:FO∥EG,
∴四边形EFOG为平行四边形.
点评 此题主要考查了菱形的性质以及平行四边形的判定、三角形斜边上中线的性质等知识,得出∠FEG+∠EGO=180°是解题关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
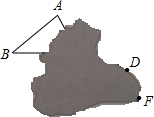 平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.
平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF. 如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.
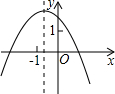
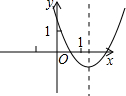
如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.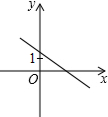 已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )
已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )