题目内容
11.已知Rt△ABC中,两直角边的和为14cm,斜边长为12cm,则这个直角三角形的面积为13.分析 设两直角边分别为a,b,则a+b=12,再根据勾股定理得出a2+c2=122,2ab=(a+b)2-(a2+b2)=142-122=52,根据三角形的面积公式即可得出结论.
解答 解:设两直角边分别为a,b,则a+b=12,
∵a2+c2=122,2ab=(a+b)2-(a2+b2)=142-122=52,
∴ab=26,
∴S△ABC=$\frac{1}{2}$ab
=$\frac{1}{2}$×26
=13.
故答案为:13.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
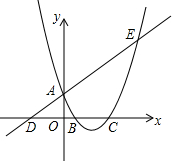 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0). 如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.
如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.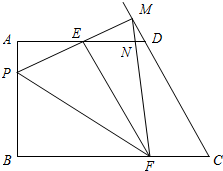 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是上底AD的中点,P是腰AB上一动点,联结PE并延长,交射线CD于点M,作EF⊥PE,交下底BC于点F,联结MF交AD于点N,联结PF,AB=AD=4,BC=6,点A、P之间的距离为x,△PEF的面积为y.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是上底AD的中点,P是腰AB上一动点,联结PE并延长,交射线CD于点M,作EF⊥PE,交下底BC于点F,联结MF交AD于点N,联结PF,AB=AD=4,BC=6,点A、P之间的距离为x,△PEF的面积为y.