题目内容
 如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是
如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是考点:圆的综合题
专题:规律型
分析:作O1M⊥OA于M,O1N⊥OC于N,作O2P⊥O1N于P,O2Q⊥O1M于Q,如图,设⊙O1的半径为R1,⊙O,2的半径为R2,⊙On的半径为Rn,根据⊙O1与半径OA、OC和弧AC都相切得到O1M=O1N=O1F=R1,点O、O1和E共线,则四边形OMO1N为正方形,利用OE=OO1+O1E,OO1=
O1M得到
R1+R1=R,解得R1=(
-1)R,同理可得R2=(
-1)R1,所以R2=(
-1)2R,按此规律即可得到Rn=(
-1)nR.
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:作O1M⊥OA于M,O1N⊥OC于N,作O2P⊥O1N于P,O2Q⊥O1M于Q,如图,设⊙O1的半径为R1,⊙O,2的半径为R2,⊙On的半径为Rn,
∵⊙O1与半径OA、OC和弧AC都相切,
∴O1M=O1N=O1F=R1,点O、O1和E共线,
∵AB⊥CD,
∴∠AOC=90°,
∴四边形OMO1N为正方形,
∵OE=OO1+O1E,
而OO1=
O1M,
∴
R1+R1=R,
∴R1=(
-1)R,
同理可得O2E=O1O2+O2E,
∴
R2+R2=R1,
∴R2=(
-1)R1,
∴R2=(
-1)2R,
…,
∴Rn=(
-1)nR.
故答案为(
-1)R,(
-1)nR.
∵⊙O1与半径OA、OC和弧AC都相切,
∴O1M=O1N=O1F=R1,点O、O1和E共线,
∵AB⊥CD,
∴∠AOC=90°,

∴四边形OMO1N为正方形,
∵OE=OO1+O1E,
而OO1=
| 2 |
∴
| 2 |
∴R1=(
| 2 |
同理可得O2E=O1O2+O2E,
∴
| 2 |
∴R2=(
| 2 |
∴R2=(
| 2 |
…,
∴Rn=(
| 2 |
故答案为(
| 2 |
| 2 |
点评:本题考查了圆的综合题:熟练掌握切线性质、两圆相切的性质和等腰直角三角形的性质.

练习册系列答案
相关题目
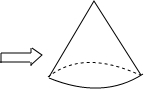 如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )
如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )| A、2cm | ||
B、2
| ||
| C、4cm | ||
D、4
|
当a<0时,方程ax2+bx+c=0无实数根,则二次函数y=ax2+bx+c的图象一定在( )
| A、x轴上方 | B、x轴下方 |
| C、y轴右侧 | D、y轴左侧 |
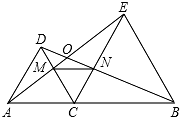 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.其中,正确的结论个数是( )
| A、5个 | B、4个 | C、3个 | D、2个 |
 如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )
如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )| A、65° | B、35° |
| C、80° | D、70° |
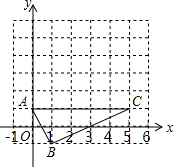 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).