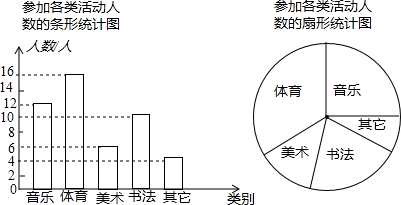
题目内容
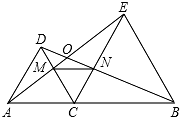 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③△ECM≌△BCN;④∠AOD=60°;⑤AC=DN.其中,正确的结论个数是( )
| A、5个 | B、4个 | C、3个 | D、2个 |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:证明AC=DC,EC=BC,∠ACD=∠BCE,借助SAS公理即可证明①成立;借助ASA定理即可证明②、③成立;借助四点共圆即可证明④成立.⑤不成立.
解答: 解:∵△DAC和△EBC均是等边三角形,
解:∵△DAC和△EBC均是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE=60°;
∴∠MCN=180°-60°-60°=60°;
在△ACE与△DCB中,
,
∴△ACE≌△DCB(SAS),
故①正确;
∵△ACE≌△DCB,
∴∠MAC=∠NDC;在△ACM与△DCN中,
,
∴△ACM≌△DCN(ASA),
故②正确;
同理可证△ECM≌△BCN;
故③正确;
∵∠OAC=∠ODC,
∴O、D、A、C四点共圆,
∴∠AOD=∠ACD=60°,
故④正确;
故选B.
 解:∵△DAC和△EBC均是等边三角形,
解:∵△DAC和△EBC均是等边三角形,∴AC=DC,EC=BC,∠ACD=∠BCE=60°;
∴∠MCN=180°-60°-60°=60°;
在△ACE与△DCB中,
|
∴△ACE≌△DCB(SAS),
故①正确;
∵△ACE≌△DCB,
∴∠MAC=∠NDC;在△ACM与△DCN中,
|
∴△ACM≌△DCN(ASA),
故②正确;
同理可证△ECM≌△BCN;
故③正确;
∵∠OAC=∠ODC,
∴O、D、A、C四点共圆,
∴∠AOD=∠ACD=60°,
故④正确;
故选B.
点评:该题以等边三角形为载体,主要考查了全等三角形的判定及其性质的应用问题;牢固掌握全等三角形的判定及其性质是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
在-0.101001,
,
,-
,0中,无理数的个数是( )
| 7 |
| 1 |
| 4 |
| π |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
| A、相切两圆的连心线经过切点 |
| B、长度相等的两条弧是等弧 |
| C、平分弦的直径垂直于弦 |
| D、相等的圆心角所对的弦相等 |
 如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是
如图所示,在半径为R的⊙O中,作直径AB、CD互相垂直,并把圆分成四个面积相等的扇形,在⊙O左上角的扇形OAC内再作⊙O1,使其与半径OA、OC和弧AC都相切;依此法继续作⊙O2、⊙O3…,请问所作的⊙O1的半径是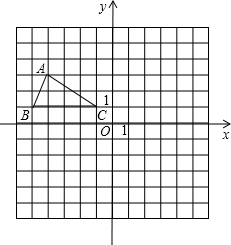 如图,点A(-4,3),将△ABC绕点O旋转180°得到△A′B′C′.
如图,点A(-4,3),将△ABC绕点O旋转180°得到△A′B′C′.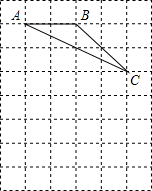 如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.