题目内容
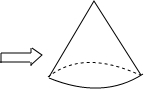如图，现有一个半径为8cm的半圆形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），该圆锥的高为（ ）| A、2cm | ||
B、2
| ||
| C、4cm | ||
D、4
|
考点：圆锥的计算
专题：
分析：已知半径为8 cm，圆心角为180°的扇形，就可以求出扇形的弧长，即圆锥的底面周长，从而可以求出底面半径，因为圆锥的高与底面半径、圆锥母线构成直角三角形的三边，就可以根据勾股定理求出圆锥的高．
解答：解：扇形弧长为：l=πr=8πcm，
设圆锥底面半径为r，
则：2πr=8π，所以，r=4，
因为圆锥的高与底面半径、圆锥母线构成直角三角形的三边，
设圆锥高为h，所以h2+r2=82，
即：h2=64-16，
解得h=4
cm．
故选D．
设圆锥底面半径为r，
则：2πr=8π，所以，r=4，
因为圆锥的高与底面半径、圆锥母线构成直角三角形的三边，
设圆锥高为h，所以h2+r2=82，
即：h2=64-16，
解得h=4
| 3 |
故选D．
点评：本题考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．
练习册系列答案
教材全解字词句篇系列答案
相关题目
下面去括号中错误的是（ ）
| A、a+（b-c）=a+b-c |
| B、m+2（p-q）=m+2p-2q |
| C、a-（b+c-d）=a-b-c-d |
| D、x-3（y+z）=x-3y-3z |
减去2-3x等于6x2-3x-8的式子是（ ）
| A、6（x2-x）-10 |
| B、6x2-10 |
| C、6x2-6 |
| D、6（x2-x-1） |
在-0.101001，
，
，-
，0中，无理数的个数是（ ）
| 7 |
| 1 |
| 4 |
| π |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示，在半径为R的⊙O中，作直径AB、CD互相垂直，并把圆分成四个面积相等的扇形，在⊙O左上角的扇形OAC内再作⊙O1，使其与半径OA、OC和弧AC都相切；依此法继续作⊙O2、⊙O3…，请问所作的⊙O1的半径是