题目内容
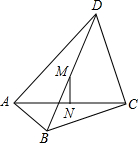 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.(1)求证:MN⊥AC.
(2)求MN的长.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)连接AM、CM,根据直角三角形斜边上的中线等于斜边的一半可得AM=CM=BM=DM=
BD,再根据等腰三角形三线合一的性质证明;
(2)利用勾股定理类似求出BD,再求出AM、AN,再利用勾股定理列式计算即可得解.
| 1 |
| 2 |
(2)利用勾股定理类似求出BD,再求出AM、AN,再利用勾股定理列式计算即可得解.
解答: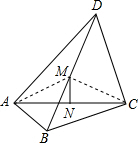 (1)证明:如图,连接AM、CM,
(1)证明:如图,连接AM、CM,
∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=CM=BM=DM=
BD,
∵N是AC的中点,
∴MN⊥AC;
(2)解:∵∠BCD=90°,BC=6,CD=8,
∴BD=
=
=10,
∴AM=
×10=5,
∵AC=6,N是AC的中点,
∴AN=
×6=3,
∴MN=
=
=4.
 (1)证明:如图,连接AM、CM,
(1)证明:如图,连接AM、CM,∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=CM=BM=DM=
| 1 |
| 2 |
∵N是AC的中点,
∴MN⊥AC;
(2)解:∵∠BCD=90°,BC=6,CD=8,
∴BD=
| BC2+CD2 |
| 62+82 |
∴AM=
| 1 |
| 2 |
∵AC=6,N是AC的中点,
∴AN=
| 1 |
| 2 |
∴MN=
| AM2-AN2 |
| 52-32 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理并作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
相关题目
方程
=
去分母后可得( )
| x-3 |
| 2 |
| 1+2x |
| 6 |
| A、3x-3=1+2x |
| B、3x-9=1+2x |
| C、3x-3=2+2x |
| D、3x-12=2+4x |
 在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC.
在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC. 如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数.
如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数.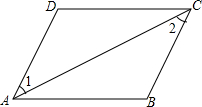 如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=2∠DAB.其中,正确的结论有( )
如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=2∠DAB.其中,正确的结论有( ) 如图,直线a∥b,∠3=131°,求∠1,∠2的度数.
如图,直线a∥b,∠3=131°,求∠1,∠2的度数. 画图(不用写作法,要保留作图痕迹)尺规作图:求作∠AOB的角平分线OC.
画图(不用写作法,要保留作图痕迹)尺规作图:求作∠AOB的角平分线OC.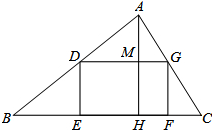 如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长.
如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长.