题目内容
15．
如图，?ABCD的对角线交于点O，且CD=4，若它的对角线的和是32，则△AOB的周长为（ ）| A． | 18 | B． | 20 | C． | 22 | D． | 24 |
分析 由平行四边形的性质得出OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AB=CD=4，求出OA+OB=16，即可得出结果．
解答 解：∵四边形ABCD是平行四边形，
∴OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AB=CD=4，
∵AC+BD=32，
∴OA+OB=$\frac{1}{2}$（AC+BD）=16，
∴△AOB的周长=OA+OB+AB=16+4=20；
选：B．
点评 本题考查了平行四边形的性质、三角形周长的计算；熟练掌握平行四边形的性质，求出OA+OB是解决问题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
5．如果把分式$\frac{x+y}{xy}$中的x、y同时扩大2倍，那么该分式的值（ ）
| A． | 为原来的2倍 | B． | 为原来的$\frac{1}{2}$ | C． | 不变 | D． | 为原来的$\frac{1}{4}$ |
如图，已知A、B两个村庄的坐标分别为（2，3），（6，4），一辆汽车从原点O出发在x轴上行驶．
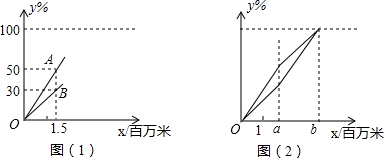
如图，抛物线y1=-$\frac{1}{2}$x2+bx+c经过点A（4，0）和B（1，0），与y轴交于点C．