Question

3．二轮自行车的后轮磨损比前轮要大，当轮胎的磨损度（%）达到100时，轮胎就报废了，当两个轮的中的一个报废后，自行车就不可以继续骑行了．过去的资料表明：把甲、乙两个同质、同型号的新轮胎分别安装在一个自行车的前、后轮上后，甲、乙轮胎的磨损度（%）y₁、y₂与自行车的骑行路程x （百万米）都成正比例关系，如图（1）所示：
（1）线段OB表示的是甲（填“甲”或“乙”），它的表达式是y=20x（不必写出自变量的取值范围）；
（2）求直线OA的表达式，根据过去的资料，这辆自行车最多可骑行多少百万米？
（3）爱动脑筋的小聪，想了一个增大自行车骑行路程的方案：如图（2），当自行车骑行a百万米后，我们可以交换自行车的前、后轮胎，使得甲、乙两个轮胎在b百万米处，同时报废，请你确定方案中a、b的值．

Answer 1

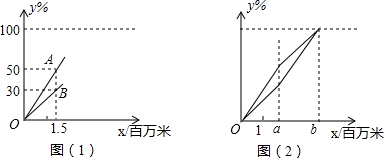
分析 （1）根据图象可得OB表示的轮胎比OA表示的轮胎磨损慢，据此即可确定是甲或乙，利用待定系数法即可求得函数解析式；
（2）利用待定系数法求得OA的函数解析式，然后求得当y=100时对应的x的值即可；
（3）根据两个轮胎的磨损度都是100，即可列出方程组求解．

解答 解：（1）线段OB表示的是甲，设OB的解析式是y=kx，
则1.5k=30，
解得：k=20，
则OB的表达式是y=20x．
故答案是：甲，y=20x；

（2）设直线OA的表达式为y=mx，
根据题意得：1.5m=50，
解得：m=$\frac{100}{3}$，
则OA的解析式是y=$\frac{100}{3}$x．
当y=100时，100=$\frac{100}{3}$x，
解得：x=3．
答：这辆自行车最多可骑行3百万米．

（3）根据题意，得
$\left\{\begin{array}{l}{\frac{100}{3}a+20（b-a）=100}\\{20a+\frac{100}{3}（b-a）=100}\end{array}\right.$，
解这个方程组，得$\left\{\begin{array}{l}{a=\frac{15}{8}}\\{b=\frac{15}{4}}\end{array}\right.$．

点评 本题考查了二元一次方程组的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系，准确的找到等量关系并用方程组表示出来是解题的关键．