题目内容
5. 已知:二次函数y=ax2+bx+c的图象经过(-3,0)、(1,0)、(0,-3)三点,
已知:二次函数y=ax2+bx+c的图象经过(-3,0)、(1,0)、(0,-3)三点,(1)求:二次函数的表达式;
(2)求:二次函数的对称轴、顶点坐标,并画出此二次函数的图象.
分析 (1)设交点式二次函数解析式为:y=a(x-1)(x+3),然后把(0,-3)代入求出a即可;
(2)把(1)中解析式配成顶点式,然后根据二次函数的性质得到二次函数的对称轴、顶点坐标,然后利用描点法画函数图象.
解答 解:(1)∵二次函数的图象经过(-3,0)、(1,0)两点
∴设二次函数解析式为:y=a(x-1)(x+3)
又∵图象经过(0,-3)点,
∴-3=a(0-1)(0+3)解得a=1
∴二次函数解析式为:y=x2+2x-3;
(2)∵y=x2+2x-3=(x+1)2-4,
∴二次函数图象的对称轴为直线x=-1;顶点坐标为:(-1,-4);
如图,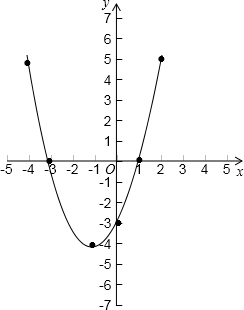
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的图象.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
15.计算$\frac{b}{a}$•$\frac{{a}^{2}-a}{b}$的结果是( )
| A. | a+1 | B. | a-1 | C. | ab-1 | D. | ab-b |
13.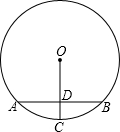 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
20.某农场经过两年的时间将产量从200万斤提高到260万斤,其中第二年增产的百分率是第一年的2倍.设第一年增产的百分率为x,则可列方程为( )
| A. | 200(1+x)(1+2x)=260 | B. | 200(1+2x)2=260 | ||
| C. | 200(1+x)+200(1+2x)2=260 | D. | 200(1+x)2=260 |
17.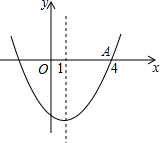 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=1,若其与x轴的一个交点为A(4,0),则由图象可知,该二次函数与x轴的另一个交点坐标是( )| A. | (-4,0) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
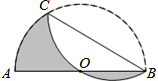 如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)
如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)