题目内容
16.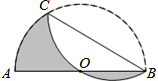 如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)
如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是6π.(结果保留π)
分析 过点O作OD⊥BC于点D,交$\widehat{BC}$于点E,则可判断点O是$\widehat{BC}$的中点,由折叠的性质可得OD=$\frac{1}{2}$OE=$\frac{1}{2}$R=3,在Rt△OBD中求出∠OBD=30°,继而得出∠AOC,求出扇形AOC的面积即可得出阴影部分的面积.
解答 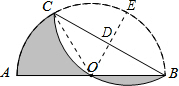 解:过点O作OD⊥BC于点D,交$\widehat{BC}$于点E,连接OC,
解:过点O作OD⊥BC于点D,交$\widehat{BC}$于点E,连接OC,
则点E是$\widehat{BEC}$的中点,由折叠的性质可得点O为$\widehat{BOC}$的中点,
∴S弓形BO=S弓形CO,
在Rt△BOD中,OD=DE=$\frac{1}{2}$R=3,OB=R=6,
∴∠OBD=30°,
∴∠AOC=60°,
∴S阴影=S扇形AOC=$\frac{60π×{6}^{2}}{360}$=6π.
故答案为6π.
点评 本题考查了扇形面积的计算,解答本题的关键是作出辅助线,判断点O是$\widehat{BOC}$的中点,将阴影部分的面积转化为扇形的面积.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:
由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为-90km,流动加油车出发位置为-80km;
(2)当两车同时开出x小时时,甲车位置为190-40xkm,流动加油车位置为-80+50x km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
| 时间(h) | 0 | 5 | 7 | x |
| 甲车位置(km) | 190 | -10 | ||
| 流动加油车位置(km) | 170 | 270 |
(1)甲车开出7小时时的位置为-90km,流动加油车出发位置为-80km;
(2)当两车同时开出x小时时,甲车位置为190-40xkm,流动加油车位置为-80+50x km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
4.下列等式成立的是( )
| A. | (-$\frac{2}{3}$)-2=$\frac{4}{9}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C. | 0.00061=6.1×10-5 | D. | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
6.已知b>0时,二次函数y=ax2+bx+a2-4的图象如下列四个图之一所示,根据图象分析,a的值等于( )


| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 已知:二次函数y=ax2+bx+c的图象经过(-3,0)、(1,0)、(0,-3)三点,
已知:二次函数y=ax2+bx+c的图象经过(-3,0)、(1,0)、(0,-3)三点, “中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过60千米/时.这时一辆小汽车在一条城市街道直路上行驶,某一时刻刚好行驶到路对面车速检测仪A正前方50米C处,过了8秒后,测得小汽车位置B与车速检测仪A之间的距离为130米,这辆小汽车超速了吗?请说明理由.
“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过60千米/时.这时一辆小汽车在一条城市街道直路上行驶,某一时刻刚好行驶到路对面车速检测仪A正前方50米C处,过了8秒后,测得小汽车位置B与车速检测仪A之间的距离为130米,这辆小汽车超速了吗?请说明理由.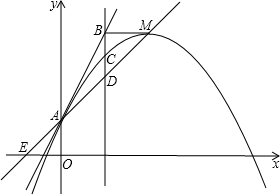 如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE.
如图,无论非零的a取何值,抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上(E、A分别在x轴、y轴上),且OA=OE. 已知:如图,点D是AB的中点,点E是BC的中点,且AB=6cm,CE=2cm.求线段DE的长.
已知:如图,点D是AB的中点,点E是BC的中点,且AB=6cm,CE=2cm.求线段DE的长.