题目内容
已知a、b、c为三角形的三边长,且满足|a-5|+
+(c-13)2=0,试判断该三角形的形状.
|
考点:勾股定理的逆定理,非负数的性质:绝对值,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:首先根据非负数的性质可得a-5=0,
b-6=0,c-13=0,再解出a、b、c的值,利用勾股定理逆定理可得该三角形是直角三角形.
| 1 |
| 2 |
解答:解:由题意得:a-5=0,
b-6=0,c-13=0,
解得:a=5,b=12,c=13,
∵52+122=132,
∴该三角形是直角三角形.
| 1 |
| 2 |
解得:a=5,b=12,c=13,
∵52+122=132,
∴该三角形是直角三角形.
点评:此题主要考查了勾股定理逆定理,以及非负数的性质,关键是掌握绝对值、算术平方根和偶次幂都具有非负性.

练习册系列答案
相关题目
满足下列条件的△ABC,不是直角三角形的是( )
| A、b2=a2-c2 |
| B、a:b:c=3:4:5 |
| C、∠C=∠A-∠B |
| D、∠A:∠B:∠C=3:4:5 |
下列各式运算正确的是( )
A、
| ||||
B、
| ||||
C、1÷b×
| ||||
D、
|
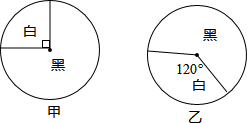 游戏组织者用如图所示的甲,乙两个转盘设计了一个游戏,规定:游戏参与者交1元钱可以分别转动甲,乙两个转盘各一次,若转盘停止时两指针的指向为下表中的组合:
游戏组织者用如图所示的甲,乙两个转盘设计了一个游戏,规定:游戏参与者交1元钱可以分别转动甲,乙两个转盘各一次,若转盘停止时两指针的指向为下表中的组合: