题目内容
1.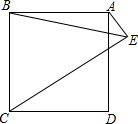 如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.(1)求∠AEB的度数;
(2)求证:AE+CE=$\sqrt{2}$BE.
分析 (1)过点B作BF⊥BE交EC延长线于F,由∠BEC=45°得BF=BE,根据四边形ABCD是正方形得AB=BC、∠ABE=∠CBF,依据“SAS”证△ABE≌△CBF可得∠AEB=∠F=45°;
(2)由△ABE≌△CBF知CF=AE,在RT△BEF中,由勾股定理得EF=EC+CF=$\sqrt{2}$BE,即AE+CE=$\sqrt{2}$BE.
解答 (1)解:过点B作BF⊥BE交EC的延长线于F,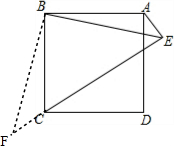
∵∠BEC=45°,
∴∠F=45°,
∴∠F=∠BEC,
∴BF=BE,
又∵四边形ABCD是正方形,
∴AB=BC,
∵∠ABC=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
∵$\left\{\begin{array}{l}{BE=BF}\\{∠ABE=∠CBF}\\{AB=CB}\end{array}\right.$,
∴△ABE≌△CBF(SAS),
∴∠AEB=∠F=45°;
(2)证明:∵△ABE≌△CBF,
∴CF=AE,
在Rt△BEF中,
∵BE2+BF2=EF2,
∴$\sqrt{2}$BE=EF,
∴AE+CE=$\sqrt{2}$BE.
点评 本题主要考查全等三角形的判定与性质,通过构建全等三角形将待求角转换到求另一个相等角是解题关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为1:4.
如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为1:4.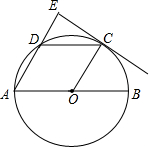 如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.
如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.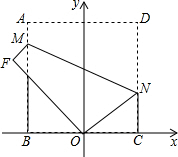 如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.
如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.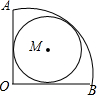 如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$.
如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$.