题目内容
9.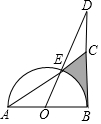 如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.
如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.(1)求弦AE的长;
(2)求阴影部分面积.
分析 (1)连接BE,根据切线的性质求出∠ABD=90°,求出BE=OB=2,△OEB是等边三角形,根据等边三角形的性质得出∠EOB=60°,BE=OB=2,根据勾股定理求出即可;
(2)分别求出△BEC、△EOB和扇形EOB的面积,即可得出答案.
解答 解:(1)连接BE,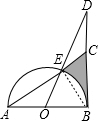
∵BD是⊙O的切线,
∴∠ABD=90°,
∵∠D=30°,
∴∠DOB=60°,
∵OB=OE=OA,直径AB=4,
∴BE=OB=2,△OEB是等边三角形,
∴∠EOB=60°,BE=OB=2,
∵AB为直径,
∴∠AEB=90°,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$;
(2)∵∠EOB=60°,
∴∠A=$\frac{1}{2}∠EOB$=30°,
∴在Rt△ABC中,cosA=$\frac{AB}{AC}$,
∴AC=$\frac{AB}{cos30°}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{8\sqrt{3}}{3}$,CE=$\frac{8\sqrt{3}}{3}$-2$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$,
∵S△BCE=$\frac{1}{2}BE×EC$=$\frac{1}{2}×2×\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴S△EOB=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$,
S扇形EOB=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,
∴S阴影=S△BCE+S△EOB-S扇形EOB=$\frac{2\sqrt{3}}{3}$+$\sqrt{3}$-$\frac{2π}{3}$=$\frac{5\sqrt{3}-2π}{3}$.
点评 本题考查了切线的性质,扇形的面积和三角形的面积计算,圆周角定理,等边三角形的性质和判定等知识点,能求出△EOB是等边三角形是解此题的关键.

| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
| A. | -1 | B. | -2 | C. | -$\sqrt{2}$ | D. | -$\frac{4}{3}$ |
| A. | 2x3 | B. | x5 | C. | x6 | D. | x9 |
| A. | (-2x2y)3=8x6y3 | B. | a6+a3=a9 | C. | (a+b)2=a2+b2 | D. | x7÷x2=x5 |
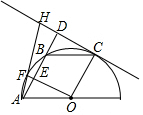 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H. 如图,在数轴上点A表示的数为$\sqrt{3}$,点B表示的数为6.2,点A、B之间表示整数的点共有( )个.
如图,在数轴上点A表示的数为$\sqrt{3}$,点B表示的数为6.2,点A、B之间表示整数的点共有( )个.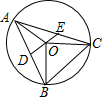 如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )
如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )