题目内容
14.求证:等腰三角形底边中线上任意一点到两腰的距离相等.分析 根据题意画出图形,写出已知与求证,然后证明:由AB=AC,D为BC中点,利用等腰三角形的“三线合一”性质得到AD为顶角的平分线,根据角平分线上的点到角两边的距离相等即可得到DE=DF得证.
解答  解:已知:如图,在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,
解:已知:如图,在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,
求证:PE=PF;
证明:∵AB=AC,AD为BC边上的中线,
∴AD平分∠BAC,
∵PE⊥AB,PF⊥AC,
∴PE=PF.
点评 本题主要考查等腰三角形的性质的应用,关键是掌握等腰三角形的腰相等且底边上的两个角相等,及角平分线上的点到角两边的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列语句中,不是命题的是( )
| A. | 经过一个点画一条直线 | B. | 两点之间,线段最短 | ||
| C. | 同角的余角相等 | D. | 对顶角不相等 |
19.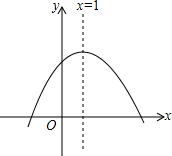 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | b<0 | ||
| C. | c>0 | D. | 方程ax2+bx+c=0有两个实数根 |
3.
某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量的关系如表格所示. 根据以上表格提供的信息,解答下列问题:
如果两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率($\sqrt{2}$取1.41).
| 个人月收入(元) | 1600 | 2400 | 3200 | 4000 | 4800 | … |
| 每月销售量(万件) | 1 | 2 | 3 | 4 | 5 | … |
如果两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率($\sqrt{2}$取1.41).
4.据悉,2015年9月,中国在西雅图购进了美国波音公司300架客机,价值38 000 000 000美元.用科学记数法表示这一数据为( )
| A. | 3.8×109 | B. | 3.8×1010 | C. | 3.8×1011 | D. | 3.8×108 |
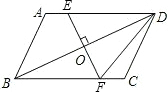 已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.
已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.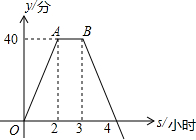 为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示
为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示