题目内容
11.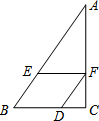 如图,已知四边形BDEF是平行四边形,AE=5,BE=2,DC=1,求EF的长度.
如图,已知四边形BDEF是平行四边形,AE=5,BE=2,DC=1,求EF的长度.
分析 由四边形BDEF是平行四边形,可得FD∥AB,EF∥BC,EF=BD,然后由平行线分线段成比例定理,求得$\frac{BD}{CD}=\frac{AF}{CF}=\frac{AE}{BE}=\frac{5}{2}$,继而求得答案.
解答 解:∵四边形BDEF是平行四边形,
∴FD∥AB,EF∥BC,EF=BD,
∴$\frac{BD}{CD}=\frac{AF}{CF}=\frac{AE}{BE}=\frac{5}{2}$,
∴BD=$\frac{5}{2}$CD=$\frac{5}{2}$×1=$\frac{5}{2}$,
∴EF=$\frac{5}{2}$.
点评 此题考查了平行线分线段成比例定理以及平行四边形的性质.注意掌握线段的对应关系.

练习册系列答案
相关题目
19.正方体的截面中,边数最多的多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
6.用四舍五入法,把数4.803保留三个有效数字,得到的近似数是( )
| A. | 4.8 | B. | 4.80 | C. | 4.803 | D. | 5.0 |
16.下列说法其中正确的个数有( )
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.下列命题中,正确的是( )
| A. | 形状相同的两个三角形是全等形 | B. | 面积相等的两个三角形全等 | ||
| C. | 周长相等的两个三角形全等 | D. | 周长相等的两个等边三角形全等 |
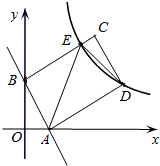 如图,矩形ABCD的顶点A、B分别在x轴、y轴上,AD=2AB,直线AB的解析式为y=-2x+4,双曲线y=$\frac{k}{x}$(x>0)经过点D,与BC边相交于点E.
如图,矩形ABCD的顶点A、B分别在x轴、y轴上,AD=2AB,直线AB的解析式为y=-2x+4,双曲线y=$\frac{k}{x}$(x>0)经过点D,与BC边相交于点E. 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$.