题目内容
1.如图,己知线段AB上,顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,CE=56,求BD的长.
分析 根据点C、D、E把线段AB分成2:3:4:5四部分,CE=56,于是求出AB=112,即可求得BD=$\frac{4+5}{2+3+4+5}$×112=72.
解答 解:∵点C、D、E,把线段AB分成2:3:4:5四部分,CE=56,
∴CE=$\frac{3+4}{2+3+4+5}$×AB=56,
∴AB=112,
∴BD=$\frac{4+5}{2+3+4+5}$×112=72.
点评 本题考查了两点间的距离,按比例分配,首先明确线段间的相互关系,把线段的比转化线段之间的倍分关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如果规定符号“?”的意义为a?b=$\frac{a×b}{a+b}$,则2?(-3)的值是( )
| A. | 6 | B. | -6 | C. | $\frac{6}{5}$ | D. | $-\frac{6}{5}$ |
6.已知三角形的两边长分别为5cm和11cm,则下列长度的四条线段中能作为第三边的是( )
| A. | 16cm | B. | 9cm | C. | 6cm | D. | 5cm |
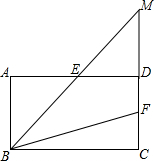 如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.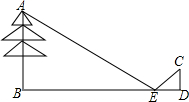 如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米.
如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米.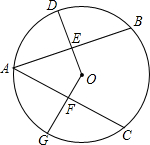 如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF.
如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.
如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.